Векторы на плоскости и в пространстве.
Векторы
Лекция 3. Векторы. Системы линейных уравнений.
Методы оценки и снижения рисков
Классификация рисков
Хозяйственный риск: понятие, причины его возникновения и последствия.
Дифференцированные и обобщающие (комплексные) показатели эффективности производства: порядок определения.
Классификация и формы выражения экономического эффекта, результата, ресурсов и затрат.
Принципы измерения экономической эффективности производства.
Сущность экономической эффективности производства.
Тема 4.5. Экономическая эффективность производства
Методы оценки стоимости имущества организации: затратный, сравнительный, доходный.
Процесс оценки имущества предприятия: основные этапы и принципы.
Сущность экономической эффективности производства. Принципы измерения экономической эффективности производства.
Классификация и формы выражения экономического эффекта, результата, ресурсов и затрат. Дифференцированные и обобщающие (комплексные) показатели эффективности производства: порядок определения. Хозяйственный риск: понятие, причины его возникновения и последствия. Классификация рисков. Методы оценки и снижения рисков.
Цельизучения темы состоит в обобщении понятия вектора, с которым студенты знакомы по школьной программе и расширение ее систематического кругозора.
Вектор– это направленный отрезок  . Точка А – начало вектора, точка В – конец вектора (рис. 3.1.1). Можно использовать обозначение
. Точка А – начало вектора, точка В – конец вектора (рис. 3.1.1). Можно использовать обозначение 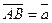 .
.
 Длиной (модулем) вектора
Длиной (модулем) вектора  называется число, равное длине вектора. Обозначается модуль вектора символом
называется число, равное длине вектора. Обозначается модуль вектора символом 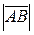 или
или 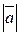 . Если модуль вектора
. Если модуль вектора 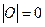 , вектор называется нулевым; направление нулевого вектора произвольно.
, вектор называется нулевым; направление нулевого вектора произвольно.
Два вектора называются коллинеарными, если они параллельны одной прямой (или лежат на одной прямой), в этом случае пишут 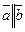 . Нулевой вектор коллинеарен любому вектору.
. Нулевой вектор коллинеарен любому вектору.
Два вектора равны, то есть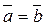 , если выполняется три условия:
, если выполняется три условия: 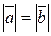 ;
; 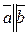 и
и 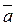 и
и 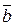 одинаково направлены.
одинаково направлены.
Произведением вектора ā на число (скаляр) λ называется вектор 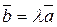 , удовлетворяющий следующим условиям:
, удовлетворяющий следующим условиям: 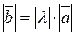 , векторы
, векторы 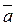 и
и 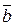 сонаправлены, если
сонаправлены, если  и направлены в противоположные стороны, если
и направлены в противоположные стороны, если  . Если
. Если  , вектор
, вектор  называется противоположным вектору
называется противоположным вектору 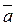 .
.
Таким образом, условие 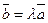 является достаточным для коллинеарности вектором
является достаточным для коллинеарности вектором 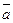 и
и 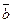 ;
;
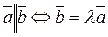
Сложение векторов. Суммой двух векторов 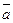 и
и 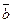 называется вектор
называется вектор  , начало которого совпадает с началом вектора
, начало которого совпадает с началом вектора 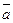 , а конец – с концом вектора
, а конец – с концом вектора 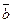 при условии, что начало вектора
при условии, что начало вектора 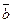 совпадает с концом вектора
совпадает с концом вектора 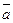 (правило треугольника) (см. рис. 3.1.2).
(правило треугольника) (см. рис. 3.1.2).
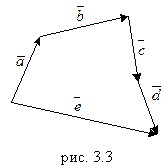
 Так как вектор
Так как вектор 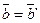 , то для получения суммы двухвекторов можно использовать правило параллелограмма: суммой двух векторов
, то для получения суммы двухвекторов можно использовать правило параллелограмма: суммой двух векторов 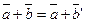 является вектор-диагональ параллелограмма, построенного на векторах
является вектор-диагональ параллелограмма, построенного на векторах 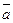 и
и 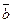 , выходящий их общего начала обоих векторов-слагаемых.
, выходящий их общего начала обоих векторов-слагаемых.
Сумма нескольких векторов находится по правилу многоугольника: чтобы найти сумму нескольких векторов  ,нужно последовательно совместить начало следующего вектора-слагаемого с концом предыдущего; тогда вектор, проведенный из начала первого вектора в конец последнего называется суммой всех данных векторов (рис. 3.1.3).
,нужно последовательно совместить начало следующего вектора-слагаемого с концом предыдущего; тогда вектор, проведенный из начала первого вектора в конец последнего называется суммой всех данных векторов (рис. 3.1.3).
 Разностьюдвух векторов
Разностьюдвух векторов  называется сумма
называется сумма 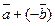 . Если вектор
. Если вектор  , то по аналогии с суммой двух векторов этот вектор является диагональю параллелепипеда, построенного на трех векторах как на сторонах (рис. 3.1.4).
, то по аналогии с суммой двух векторов этот вектор является диагональю параллелепипеда, построенного на трех векторах как на сторонах (рис. 3.1.4).
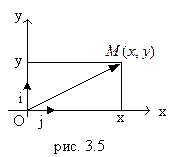 Рассмотрим вектор
Рассмотрим вектор 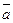 в плоскости. Перенесем в начало координат системы хОу.
в плоскости. Перенесем в начало координат системы хОу.
Получим вектор  . Координатами вектора
. Координатами вектора 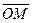 называются координаты точки М(х;у). Введем на осях координат векторы i и j – единичной длины (рис. 3.1.5).
называются координаты точки М(х;у). Введем на осях координат векторы i и j – единичной длины (рис. 3.1.5).
Очевидно, или 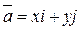 или
или 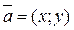 . Если вектор
. Если вектор 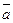 рассматривается в трехмерном пространстве, где точка М характеризуется тремя координатами, то есть M(x,y,z), то вектор
рассматривается в трехмерном пространстве, где точка М характеризуется тремя координатами, то есть M(x,y,z), то вектор 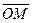 можно представить в виде:
можно представить в виде:
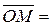 xi
xi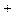 yj
yj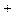 zk, (3.1.1)
zk, (3.1.1)
где i, j, k – единичные векторы, лежащие на осях координат. Пусть  ,
,  . Найдем сумму и разность этих векторов:
. Найдем сумму и разность этих векторов:
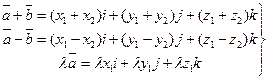 (3.1.2)
(3.1.2)
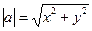 или
или 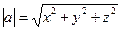
Сложение векторов и умножение вектора 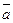 на скаляр подчиняется следующим свойствам:
на скаляр подчиняется следующим свойствам:
1) 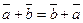 ;
;
2)  ;
;
3) 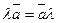 ;
;
4)  ;
;
5) 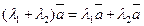 .
.
Доказательства вытекают на основании (3.1.2).

Определение. Скалярным произведением векторов 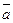 и
и 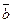 называется число
называется число 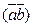 равно произведению модулей этих векторов на косинус угла φ между ними, то есть
равно произведению модулей этих векторов на косинус угла φ между ними, то есть  . (3.1.3)
. (3.1.3)
Из (3.1.3) вытекают свойства скалярного произведения:
1) 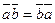 ;
;
2)  ;
;
3) 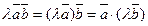 ;
;
4) если 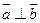 , то
, то  .
.
Используя свойства скалярного произведения, можно найти скалярное произведение двух векторов в координатной форме. Если  ,
,  , то
, то 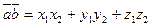 ; если
; если 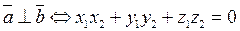 - условие перпендикулярности векторов.
- условие перпендикулярности векторов.
Если векторы коллинеарны, то есть  , то
, то  - условие коллинеарности векторов.
- условие коллинеарности векторов.
Понятие n-мерного вектора. Векторное пространство. Линейная комбинация и линейная зависимость векторов.
Понятие вектора можно обобщить.
Определение. n-мерным вектором называется упорядоченная совокупность n действительных чисел, записываемых в виде Х=(х1, х2,…, хn), хi – компоненты вектора Х.
Понятие n-мерного вектора широко используется в экономике. Например, некоторый набор товаров можно охарактеризовать вектором  , а соответствующие цены – вектором
, а соответствующие цены – вектором 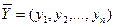 .
.
Два n-мерных вектора равны тогда и только тогда, когда равны их соответствующие компоненты:  ,
, 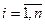 .
.
По аналогии с геометрическими векторами вводятся: сумма векторов 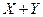 с компонентами
с компонентами 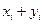 ,
, 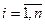 ; разность векторов
; разность векторов 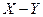 с компонентами
с компонентами 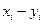 ,
, 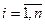 , с теми же свойствами.
, с теми же свойствами.
Скалярное произведение n-мерных векторов:
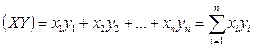 .
.
Если X - набор товаров, а Y
- набор товаров, а Y - соответствует ценам за единицу каждого товара, то стоимость всем товаров:
- соответствует ценам за единицу каждого товара, то стоимость всем товаров:
 .
.
 Определение.Множество векторов с действительными компонентами, в котором определены операции сложения (вычитания) и умножения вектора на скаляр, удовлетворяющего приведенным выше свойствам называется векторным пространством.
Определение.Множество векторов с действительными компонентами, в котором определены операции сложения (вычитания) и умножения вектора на скаляр, удовлетворяющего приведенным выше свойствам называется векторным пространством.

Определение.Вектор  называется линейной комбинацией векторов
называется линейной комбинацией векторов  векторного пространства, если
векторного пространства, если
 , (3.1.4)
, (3.1.4)
где  - любые действительные числа.
- любые действительные числа.
 Определение. Векторы
Определение. Векторы  называются линейно зависимыми, если существуют такие числа
называются линейно зависимыми, если существуют такие числа  , не равные одновременно нулю, что линейная комбинация
, не равные одновременно нулю, что линейная комбинация  .
.
В противном случае векторы  (
( ) называются линейно независимыми.
) называются линейно независимыми.
Если векторы  линейно зависимы, то хотя бы один из них линейно выражается через остальные. Покажем это. Пусть векторы
линейно зависимы, то хотя бы один из них линейно выражается через остальные. Покажем это. Пусть векторы  (
( ) линейно зависимы, то есть
) линейно зависимы, то есть
 и
и  , тогда
, тогда

Верно и обратное утверждение: если один из векторов выражается через остальные, то все векторы в совокупности линейно зависимы.
Для векторного пространства имеет место следующее свойство: если среди m векторов какая-то часть векторов являются линейно зависимыми, то все m векторов линейно зависимы.
 Определение.Векторное пространство называется n-мерным, если в нем существует ровно n линейно независимых векторов, а любые из (
Определение.Векторное пространство называется n-мерным, если в нем существует ровно n линейно независимых векторов, а любые из ( ) векторов уже линейно зависимы. Это число n называется размерностью пространства.
) векторов уже линейно зависимы. Это число n называется размерностью пространства.
