Эластичность функции

Понятие эластичности впервые было введено Аланом Маршаллом, в связи с анализом функции D.

Маршалл ставил следующую задачу, как изменится спрашиваемое количество D, если соответствующая цена P на некоторые блага изменится на 1 ед.

Рассмотрим представленную проблему математически: пусть величина y зависит от некоторого аргумента x, т. е. между ними будет существовать функциональная связь y = f(x). Вполне очевидно, что в силу этой функциональной связи изменение аргумента на всей величине Δх, приведет к изменению величины y на Δy.

Тогда возникает вопрос: — как измерить чувствительность функции y к изменению аргумента х.

Одним из методов измерения такой чувствительности служит производная функции:

Однако в экономике этот показатель неудобен, в связи с тем, что он зависит от единицы измерения.

В этой связи для изучения функции эластичности необходимо вводить безразмерную величину. Таким образом, в экономике исследуют связь не абсолютных, а относительных величин.

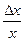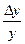Поэтому от абсолютных изменений сопоставляемых при анализе величин Δх, Δy не обходимо перейти к относительным : и соответственно.

Итак, эластичность функции 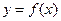показывает предел отношений относительных изменений переменных х и y.

Другими словами, эластичность функции — это безразмерная величина, которая показывает возможность функции реагировать на изменение аргумента х. Если эластичность функции y по переменной x обозначить , то используя определение эластичности, получаем:

Таким образом, эластичность— коэффициент пропорциональности между относительными изменениями аргумента и функции.

С точки зрения экономики эластичность означает: на какой процент изменится спрашиваемое количество, если цена изменится на 1%.