АНАЙНАЛЫМ БИОМЕХАНИКАСЫ.

ЖОСПАРЫ:

1. Сұйық ағынының үзіліссіздік теңдеуі.

2. Сұйықтың тұтқырлығы. Пуазейль формуласы.

3. Қанның реологиялық касиеттері.

4. Пульсті толқын. Франк үлгісі.

1. Сұйық ағынының үзіліссіздік теңдеуі.

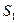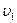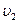Қанайналымның физикалық ерекшеліктерін талдау үшін сұйық механикасының бірқатар қағидаларын қарастыру керек. Солардың біреуі- сұйық ағынының үзіліссіздік теңдеуі. Айталық, қималары , болатын (сурет 1) түтікше арқылы сұйық ағады деп есептейік. Осы қималардағы сұйық ағынының жылдамдығы , болсын. Сонда қандайда бір қима арқылы белгілі бір уақытта ағатын сұйықтың массасы 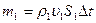, ал екінші қима арқылы осындай уақытта өтетін сұйықтың массасы 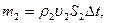болады, мұндағы әр қималардағы сұйықтың тығыздықтары.

 

 

Сурет 1. Қимасы әртүрлі құбыр арқылы сұйықтың ағысы.

 

Қалыптасқан қозғалыс үшін сұйықтың массалары (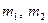) бірдей болу керек, әйтпесе 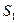, қималар арасындағы сұйықтың мөлшері арта бастаушы еді (не кемуші), және ағынның стационарлығы тоқтаушы еді. Сөйтіп, айтып отырған сұйық үшін мына қатынасты аламыз: 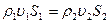; (1). Осы теңдеу сұйықағынының үзіліссіздік теңдеуідеп аталады. Сығылмайтын сұйық үшін 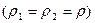ағынының үзіліссіздік теңдеуі қысқаша былай жазылады: 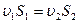; (2).

Көлденең қимасы кіші жерде, сұйықтың ағыс жылдамдығы жоғары болады. Осындай ерекшелік адамның қантамырлар жүйесінде байқалады; мысалы, барлық капиллярлар саңылауының қосынды ауданы аорта саңылауынан 500 есе үлкен. Ағынының үзіліссіздік теңдеуіне сәйкес капиллярлардағы қан ағысының жылдамдығы аортадағыға қарағанда көп есе кіші болады (сурет 2).

Сурет 2. Адамның қантамырлар жүйесінің түрлі бөліктерінде жылдамдықтардың үлестірілуі: аортадағы қан ағысының жылдамдығы (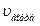) капиллярлардағымен (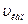) салыстырғанда үлкен.

 

Сұйықтың маңызды қасиеті- ішкі үйкелістің немесе тұтқырлықтыңболуы. Тұтқырлық күштері (ішкі үйкеліс күштері) сұйық қабаттарының салыстырмалы орын ауыстыруы кезінде пайда болады (сұйықтың бір қабаттарының екінші бір қабаттарына салыстырмалы ығысуы кезінде). Ағыннан бір- бірінен аралыққа қалып отыратын, аудандары бірдей екі параллель қабатты қарастырайық. Тәжірибе көрсеткендей, сұйықтың әр қабатына шамасы мен қабаттар ауданына пропорционал болатын күш әсер етеді.

шамасы қабаттарға перпендикуляр бағытта (Z осі бойымен) қабаттан қабатқа өтулер кезіндегі жылдамдықтың өзгеру шапшаңдығын сипаттайды.

 

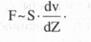(3)

 

шамасы жылдамдық градиентідеп аталады (ол шамамен - ке тең).

 

Пропорционалдық коэффициентті (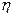) енгізе отырып,былай жазуға болады:

(4)

 

 

2. Сұйықтың тұтқырлығы. Пуазейль формуласы.

Пропорционалдық коэффициенті (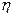) 4-ші формулаға енген шамалардың өлшем бірліктеріне байланысты болады. Пропорционалдық коэффициент сұйықтың не газдың табиғатына байланысты, ендеше ол сұйықтың не газдың тұтқырлық қасиеттерін сипаттайды. Осы коэффициент ішкі үйкеліс коэффициенті не тұтқырлық коэффициенті, кейде жәй тұтқырлық деп аталады. Тұтқырлықтың өлшем бірлігі мына қатынастан алынады: 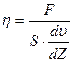; (5)

Осыдан мынадай анықтама шығады: СИ жүйесінде тұтқырлықтың өлшем бірлігінежылдамдық градиенті 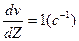, аудандары S = 1 м2 болатын сұйықтың екі қабаты арасында 1 Н-ға тең ішкі үйкеліс күші пайда болатын сұйықтың тұтқырлығы алынады. Осы бірлік Н с/ м2 деп аталады.Осылайша СГС жүйесіндегі тұтқырлықтың өлшем бірлігі анықталады, ол «Пуаз»деп аталады (Пуазейль деген ғалымның құрметіне).

Тұтқырлы сұйықтың цилиндр пішінді құбырмен ағысын қарастырайық. Құбырдың қималары бойынша сұйық жылдамдықтарының үлестірілуі мына формуламен анықталады:

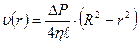; (6)

мұндағы - радиусы 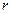, ұзындығы құбыр арқылы ағатын тұтқырлығы 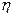болатын сұйықтың құбырдың екі ұшындағы қысымдарының айырмасы. Сұйық қабатының жылдамдығының құбырдың центріне дейінгі арақашықтыққа тәуелділігі 3-ші суретте көрсетілген: құбырдың ортасында 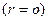жылдамдық жоғары, центрден алыстаған сайын ағыс жылдамдығы кемиді, ал құбыр қабырғасының жанында 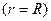жылдамдық 0-ге тең болады.

 

Сурет 3. Қима бойында ламинарлы ағысы кезіндегі

сұйық бөлшектерінің жылдамдықтарының үлестірілуі.

 

Тұтқырлы сұйықтың ағысының көлемдік жылдамдығын есептейік, көлемдік жылдамдығы дегеніміз құбырдың қимасы арқылы бірлік уақытта ағатын сұйықтың көлемі (сурет 4).

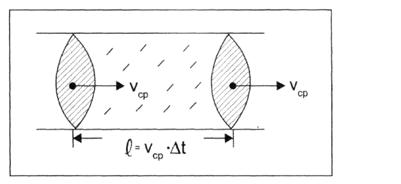
Сурет 4. S қима арқылы 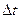уақытта ағатын сұйықтың көлемі.

 

Егер құбыр арқылы ағатын сұйықтың орташа жылдамдығы 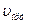болса, онда S қима бойымен уақытта ағатын сұйықтың көлемі былайша анықталады: 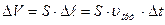; Ал бірлік уақыттағы көлемі- ;

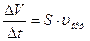Осы көлемдік жылдамдық болып табылады: 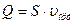; (7).

Құбыр қимасы бойымен орташа жылдамдықты Пуазейль формуласымен анықтауға болады:

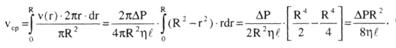(8).

 

 

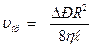
Сонда сұйықтың ағысының көлемдік жылдамдығы былайша анықталады: 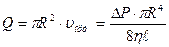; (9)

Осы (9) өрнек Пуазейль заңыдеп аталады.

Оның физикалық мағынасы: ұзындығы, радиусы R құбырдағы сұйықтың қысымдар айырмасы белгілі болғанда, сұйықтың көлемдік жылдамдығы неғұрлым кіші болса, сұйықтың тұтқырлығы соғұрлым жоғары болады.

Кейде Пуазейль заңы басқаша жазылады, яғни гидравликалық кедергі арқылы-

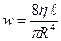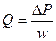; (10)

Гидравликалық кедергісұйықтың тұтқырлығымен, құбырдың ұзындығымен, радиусымен анықталады, және де радиусқа тәуелділігі өте ерекше;

Мысалы, радиустары екі есеге айрықша болатын екі құбырдың (ұзындықтары бірдей, олармен бір түрлі сұйық ағады) гидравликалық кедергілері мынадай болады:

;

(6)- шы формула бойынша, көлемдік жылдамдығы тұрақты болған кезде, құбырдың ұштарындағы қысымдардың айырмашылығы (айырмасы) гидравликалық кедергі неғұрлым үлкен болса, соғұрлым үлкен болады. Бұл адамның қантамырлар жүйесінде қысымдардың таралуын ұғынуға мүмкіндік береді. Ол үшін мынаны, барлық бөліктердегі орташа көлемдік жылдамдықтың тұрақты болатындығын назарға алу керек және аортаның, артериялардың, артериолалардың, капиллярлардың гидравликалық кедергілерінің қатынасын анықтау керек. Аортаның радиусы артериялармен салыстырғанда әлдеқайда үлкен, артериялардың радиусы артериолалардың радиусынан әлдеқайда үлкен. Осы бөліктердің гидравликалық кедергілерінің 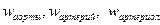арасында мынадай қатынас бар деп айтуға болады: 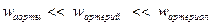(11)

Бірақ гидравликалық кедергі тек радиусқа ғана тәуелді емес, оған қантамырының ұзындығы мен саны, қанның тұтқырлығы (барлық бөліктерде ол бірдей емес) әсер етеді, және де мынаны еске алу керек: аорта- дара тамыр, ал артериялар, артериолалар, капиллярлар тармақталған көп тамырлардан тұратын жүйеболып табылады. Ендеше аортада қысымның төмендеуі өте аз болады, ал артериолаларда- аса үлкен болады.

Осы заңдылық 5-ші суретте көрсетілген. Артериолаларда қысым бастапқы шамасынан 80-85% -ға аса интенсивті төмендейді.

 

 

Сурет 5. Адамның қантамырлар жүйесінің түрлі бөліктеріндегі қысымның үлестірілуі.

3. Қанның реологиялық касиеттері.

Қан белгілі бір тұтқырлығы бар сұйық деп жорамалданған. Шындығында ол осылай емес, қан ньютондық емес сұйық, оның тұтқырлық коэффициенті көптеген факторларға байланысты болады және бір қантамырынан екінші бір қантамырына өткен кезде, тұтқырлығы өзгереді. Оның осылайша болуы қанның ішкі құрылымына байланысты. Қан ерітіндідегі, яғни плазмадағы пішінді элементтердің (эритроциттер, лейкоциттер, тромбоциттердің) суспензиясы болып табылады.

Пішінді элементтердің 93%-ы эритроциттер болып табылатындықтан, қан- натрий хлоридінің изотонды ерітіндісіндегі эритроциттердің суспензиясы деп айтуға болады. Эритроциттердің агрегаттардың түзілуіне тенденциясы бар (егер қанды шыны денеге жақса, онда жарық. микроскобымен эритроциттердің бір- бірімен жабысып, агрегаттарды («тиынды бағаналар») түзетіндігін көруге болады.

Ірі және ұсақ тамырлардағы агрегаттардың түзілу шарты түрліше. Бұл ең алдымен қантамырының, агрегаттың, эритроциттің өлшемдерінің қатынасына байланысты болады. Диаметрі үлкен болатын ірі қантамырларында эритроциттердің агрегациясы жеткілікті жоғары, ал ұсақ артериялар мен артериолаларда агрегаттар субагрегаттарға, жеке эритроциттерге ыдырайды, сөйтіп жүйенің тұтқырлығы біраз кемиді. Капиллярлардағы эритроциттердің қозғалу жағдайы айрықша өзгереді: эритроциттің диаметрі капиллярдың диаметрінен үлкен болғандықтан, эритроциттер күшті деформацияланып, күмбезге ұқсас болады. Ұсақ тамырлар қабырғаларына ығыстырылған плазма капиллярмен эритроциттердің қозғалуын қамтамасыз етеді, бірақ бұл өте қиын. Сөйтіп, түрлі тамырлардағы сұйықтың ішкі құрылымы түрліше, сондықтан қанға Пуазейль заңын жуықтап қолдануға болады; теңдеуде қантамырлар жүйесінің бөліктеріндегі тұтқырлықтың орташа мәні алыну керек.

 

4. Пульсті толқын. Франк үлгісі.

Адамның қантамырлар жүйесінің тағы бір маңызды ерекшелігі- пульсті толқынның таралуы. Пульсті толқындегеніміз сол қарыншадан аортаға қанның соққы көлемінің ығыстырылуы нәтижесінде (жүректің әр жиырылуы кезінде) ірі созылғыш тамырдың көлемінің артуының таралу үрдісі. Бір- бірімен кезектес 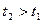екі уақыт мезетіндегі пульсті толқынның таралуының профильді кескіні 6-шы суретте көрсетілген.

Пульсті толқынның таралу жылдамдығы мына формуладан табылады: 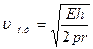; (12)

мұндағы Е- тамыр қабырғасының серпімділік модулі, 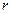- тамыр саңылауының радиусы;

 

h – тамырдың қалыңдығы;—қанның тығыздығы. Осы формулаға барлық шамалардың мәнін қойғанда, пульсті толқынның жылдамдығының мәні алынады: шамамен 6—8 м/с (бұл мән қан бөлшектерінің жылдамдығынан көп есе үлкен: аортадағы қан бөлшектерінің жылдамдығы шамамен 0,2 м /с ).

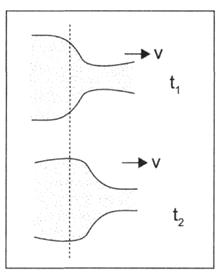
Сурет 6. Созылмалы қантамыры арқылы пульсті толқынның таралуы.

 

Пульсті толқынның таралуының тағы бір ерекшелігі- систола уақытында (ол шамамен 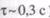- ке тең) пульсті толқын 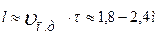аралықты жүріп өтеді.

Осы арақашықтық өте үлкен, бұл пульсті толқынның (көлемінің артуы) барлық созылмалы қантамырларын қамтитынын және осы жүйені біраз уақыт бойы кеңейген күйде ұстап тұратындығын білдіреді. Қандайда бір период өткеннен кейін аортада қысымның төмендеуі басталады.

Пульсті толқынның толық математикалық жазылуы өте қиын және громоздко. Пульсті толқынмен байланысты қиын емес математикалық үлгі Франк үлгісі деп аталады. Осы үлгі ірі созылмалы қантамырының қайсыбір нүктесіндегі қысымның уақытқа тәуелділігін жуықтап есептеуге мүмкіндік береді. Аорта клапаны жабылғаннан кейін (сол қарыншадан қан қарастырылып отырған уақытта аортаға келіп түспейді), ірі созылмалы қантамырынан ұсақ тамырларға қанның ығыстырылу фазасын қарастырайық.

Бірқатар қысқартулар жасайық:

- барлық ірі қантамырлары созылмалы қабырғалары бар бір резервуарға біріктірілген. Оның көлемі (V) қысымға (Р) пропорционал: 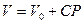(13).

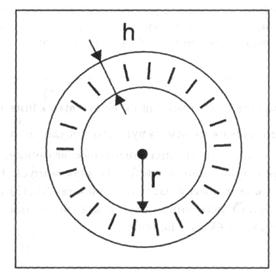
Сурет 7. Қантамырының көлденең қимасы. r- саңылау радиусы,

һ- тамыр қабырғасының қалыңдығы.

 

мұндағы С — тамырдың созылғыштығы; Vo – тамыр ішіндегі қысым атмосфералық қысымға тең болған кездегі (Р = 0) тамырдың бастапқы көлемі.

(Ірі тамырлардың гидравликалық кедергісін есепке алмаймыз, ол Пуазейль заңы бойынша кезкелген нүктедегі қысым бірдей деп есептеуге мүмкіндік береді);

- микротамырлар жүйесі үлгіде қатаң құбыр деп көрсетілген. Оның гидравликалық кедергісі өзгермейді депесептеп, ұсақ тамырлардың созылғыштығын есепке алмаймыз. Бұл Пуазейль заңын ұсақ тамырлардағы қанағысы үшін жазуға мүмкіндік береді.

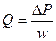(14),

мұндағы Q — ірі тамырлардан ұсақ тамырларға енетін қанның көлемдік жылдамдығы; - ірі тамыр (ұсақ тамырға енетін жердегі) мен ұсақ тамырлар жүйесінен шығатын жердегі қысымдардың айырмасы. Осы жерде тағы бір ықшамдауды орындау қажет: қысымдардың осы айырмасы ірі тамырдағы қанның қысымына шамамен тең деп есептеу керек және ұсақ тамырлар жүйесінен шығатын жердегі қысымды ескермеу керек (сурет 2);

- жүрек қызметінің белсенділігімен анықталатын аорта клапандарының ашылып, жабылуының сыртқы механизмі болады.

(13)-, (14)- ші теңдеулерді біріктіріп, 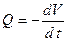(15) алынады.

(15)-ші теңдеу ағатын қанның көлемдік жылдамдығының ірі тамыр көлемінің кішірею жылдамдығына тең екендігін білдіреді (осы кезде 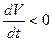; оң бөлігінде оң шама алу үшін, сол бөлігіндегі туынды алдына минус таңбасын қою керек). (13)-ші теңдеудің оң және сол жақтарынан туынды тауып, оны (15)-ші теңдеудің минус таңбасымен алынған оң жақ бөлігіне теңестіріп, (14)-ші теңдеуді ескеріп, мынаны аламыз:

 

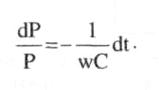(16)

Теңдеудің екі жағын интегралдап, аламыз:

Бастапқы уақыт мезетінде (t = 0) ірі тамырдағы қысым Ро болса, ал кезкелген уақыт мезетінде қысымды (16)-шы теңдеуді пайдаланып, былай жазуға болады:

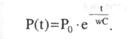(17).

Осы өрнек ірі тамырдан қанды ығыстыру периоды үшін алынған. Осы тамырдағы қанның қысымы сол қарыншадағы қысымға дейін төмендегенше, аорта клапаны ашылып, қанның келесі соққы көлемінің аортаға енуіне мүмкіндік бермейінше, (17)-ші өрнек дұрыс

болады.