Стандартные аксонометрические системы

1. Ортогональная изометрия.

В ортогональных аксонометриях показатели искажения по осям равны косинусам углов наклона координатных осей к аксонометрическим плоскостям проекций (u = cos α; v = cos β; w = cos γ,

где α, βиγ - соответственно углы наклона натуральных осей x, yиzк аксонометрическим плоскостям проекций. В изометрии показатели искажения по всем трем осям одинаковы, т.е.

u = v = w.

Из этого следует, что

cos α = cos β = cos γи α = β = γ.

Это означает, что в ортогональной изометрии натуральные координатные оси одинаково наклонены к плоскости проекций.

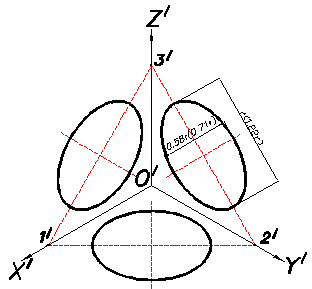
Рис.69

Из равенства углов α, βиγ следует и равенство отрезков аксонометрических осей О′1′ = О′2′ = О′3′.

Треугольник 1′2′3′получается равносторонним. Высоты таких треугольников попарно пересекаются под углом 120^о. Поэтому совпадающие с ними аксонометрические оси в ортогональной изометрии образуют между собой углы по 120^о. Как указывалось выше, в ортогональной изометрии

u = v = w.

Тогда из соотношения

u² + v²+ w² = 2

получаем 3u² = 2.Следовательно,показатели искажения по все тре осям одинаковы и равныu = v = w ≈ 0,82.

На практике пользуются приведенной ортогональной изометрией, в которой показатели искажения приводятся к единице, т.е.

U = V = W = 1.

При этом коэффициент приведения будет равен:

m = U : u = 1.22.

Это означает, что приведенная ортогональная изометрия увеличивает изображение примерно в 1.22 раза.

Построение эллипсов, изображающих окружности, расположенных в координатных плоскостях или в плоскостях, им параллельных, показано на Рис.69. Малые оси эллипсов параллельны соответствующим аксонометрическим осям, а большие оси – им перпендикулярны.

Необходимо отметить, что существует только одна ортогональная изометрия.

 

2. Ортогональная диметрия

 

 

В отличие от ортогональной изометрии ортогональных диметрий может быть построено бесчисленное множество. Одной из наиболее распространенных стандартных диметрий является диметрия, у которой

u = w; v = u : 2.

В этом случае

u² + w² + v² : 4 = 2.

Соответственно

u = w = 0.94; v = u : 2 = 0.47.

В приведенной ортогональной диметрии

U = W = 1; V = U : 2 = 0.5.

При этом коэффициент приведения будет равен

m = U : u = 1.06.

Рис.70

Приведенная ортогональная диметрия увеличивает изображение примерно в 1.06 раза.

Как и в случае с ортогональной изометрией построение эллипсов, изображающих окружности, расположенных в координатных плоскостях или в плоскостях, им параллельных, показано на Рис.70. Малые оси эллипсов параллельны соответствующим аксонометрическим осям, а большие оси – им перпендикулярны.

Более подробно стандартные аксонометрические системы описаны в учебниках.