Конволютный геликоид.
Развертывающийся геликоид
Образуется при движении прямолинейной образующей l, которая касается цилиндрической винтовой линии во всех ее точках. Данная винтовая линия является ребром возврата, поэтому развертывающиеся геликоиды также относятся к развертывающимся (торсовым) поверхностям.
Образуется при движении прямолинейной образующей l, которая пересекает цилиндрическую винтовую линию во всех ее точках и остается параллельной плоскости, перпендикулярной оси винтовой линии. (Образующая во всех своих положениях расположена под прямым углом к оси винтовой поверхности).
Лекция 5.
Поверхности вращения:
Все поверхности вращения образуются путем вращения некоторой образующей вокруг определенной оси.
Форма поверхности вращения определяется формой образующей и ее расположением относительно оси.
Состав определителя любой поверхноcти вращения
( i; l); где i – ось вращения;
l – образующая.
Закон образования поверхности вращения
l i.
Рассмотрим поверхности вращения с образующей – прямая линия.
Цилиндрическая поверхность вращения D(i, l) (Рис.30)
[образующая (прямая линия) параллельна оси вращения]
(i, l ) – определитель поверхности:
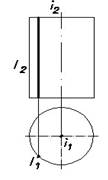 i – ось вращения;
i – ось вращения;
l – образующая.
Закон Каркаса: l i.
Данная поверхность «несет» на себе два семейства удобных для построения линий:
1. образующие – прямые линии;
2. концентрические окружности постоянного радиуса – линии, лежащие в плоскостях, перпендикулярных оси i.
Рис.30
У всех нижеприведенных поверхностей вращения составы определителей и законы образования поверхностей примерно такие же как и у вышеприведенной цилиндрической поверхности. По этой причине в этом тексте при описании этих поверхностей приводиться не будут.
Коническая поверхность вращения L(i, l) (Рис.31)
 [образующая пересекается с осью вращения (l х i )]
[образующая пересекается с осью вращения (l х i )]
Также “несет” на себе два семейства удобных для построения линий:
1. образующие – прямые линии;
2. концентрические окружности переменного радиуса (лежат в плоскостях, перпендикулярных оси вращения).
Рис.31
Однополостный гиперболоид вращения W(i, l) (Рис.32)
[(образующая скрещивается с осью вращения (l i)]
На данной поверхности имеется три семейства удобных для построения линий.
1. 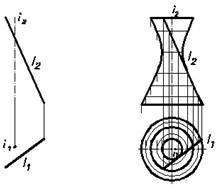 Два семейства образующих (две пересекающиеся прямые с наклоном в противоположные стороны и под одним углом к плоскости, перпендикулярной к оси вращения).
Два семейства образующих (две пересекающиеся прямые с наклоном в противоположные стороны и под одним углом к плоскости, перпендикулярной к оси вращения).
2. Концентрические окружности переменного радиуса (лежат в плоскостях, перпендикулярных оси вращения).
Если I ^ П1, фронтальным очерком однополостного гиперболоида вращения будет гипербола.
Рис.32