Линейчатые поверхности с плоскостью параллелизма

(Поверхности Каталана)

 

К ним относятся:

- цилиндроид;

- коноид;

- гиперболический параболоид.

Рассматриваемые поверхности с двумя направляющими и в каждом случае образующие параллельны одной плоскости, называемой плоскостью параллелизма.

 

Цилиндроид V( m, n, Г) (Рис.25)

 

( m, n, Г) – определитель поверхности.

Состав определителя:

m и n– направляющие (кривые линии);

Г – плоскость параллелизма.

(В данном случае плоскостью параллелизма является горизонтально - проецирующая плоскостьГ.

Рис.25 Закон образования поверхности V

(закон Каркаса):

li x m; li х n; li II Г

 

Коноид C( m, n, Г) (Рис.26)

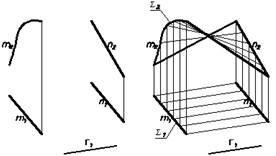( m, n, Г) – определитель поверхности.

Состав определителя:

m – направляющая (кривая линия);

n – направляющая (прямая линия);

Г – плоскость параллелизма

(плоскостью параллелизма является горизонтально-проецирующая плоскостьГ).

Закон образования поверхности C

(закон Каркаса):

Рис.26 li x m; li х n; li II Г

Если у коноида прямолинейная направляющая перпендикулярна плоскости параллелизма, такой коноид называют прямым.

 

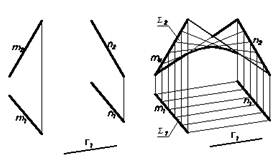Гиперболический параболоид (косая плоскость)

S (m, n,Г) (Рис.27)

(m, n,Г) - определитель.

Направляющими у гиперболического параболоида служат две скрещивающиеся прямые m и n. Г – плоскость параллелизма. Название данной поверхности обусловлено тем, что в сечении ее плоскостью, кроме прямолинейных образующих можно получить гиперболу и параболу.

Рис.27

Закон образования поверхности S (закон Каркаса):

li x m; li х n; li II Г.