Взаимное расположение прямой и плоскости

Задание плоскости на К.Ч.

Рис.13

Рис.12

Линии уровня.

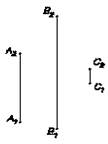
Горизонталь – линия, все точки которой имеют одинаковую координату Z(аппликата) .Рис.12

Горизонталь параллельна горизонтальной плоскости проекций.

Обозначение горизонтали – h (hIIП1).

 

На П2- Z– const (для всех точек линии).

На П1: h1=h, h1- натуральная величина прямой h.

Фронталь– линия, все точки которой имеют одинаковую координату Y (ордината). Рис.13

Фронталь параллельна фронтальной плоскости проекций.

Обозначение фронтали – f(fIIП2).

На П1 - Y – const (для всех точек прямой)

На П2 f2= f, f2- натуральная величина отрезка АВ.

Профильная линия – линия, все точки которой имеют одинаковую координату X (абсцисса).

Профильная (Рис.14) линияпараллельна профильной плоскости проекций. Обозначим профильную линию буквой п (пII П3). На П1 и П2 проекции профильной линии п совпадают с линией связи. Для описания профильной линии (прямой) на комплексном чертеже необходимо вводить профильную плоскость проекций.

Рис.14

 

 

Плоскость – простейший вид поверхности.

Плоскость – двумерный геометрический образ. Плоскости, как и все поверхности обозначаются прописными буквами греческого алфавита S,D,W,L,Y и т.д. Плоскость можно представить как совокупную последовательность положений прямой линии, перемещающейся в пространстве по двум параллельным прямым.

В отличие от точки или линии плоскость в общем случае не может быть задана своими проекциями на комплексном чертеже, т.к. горизонтальная, фронтальная и профильная проекции плоскости занимают все поле проекций П1, П2 и П3 комплексного чертежа. Поэтому для задания на К.Ч. плоскостей, а также других поверхностей введем понятие «определитель Г.О.»

Оопределитель Г.О.– сумма независимых геометрических условий, однозначно определяющих все множество точек данного Г.О. на К.Ч.

К примеру, для того, чтобы задать прямую линию на комплексном чертеже, достаточно задать на этом чертеже две точки этой линии. Таким образом, определителем прямой линии являются две точки, принадлежащие данной линии и заданные двумя своими проекциями на комплексном чертеже.

Плоскости на комплексном чертеже также могут быть заданы с помощью определителей.

 

Определители плоскостей общего положения (Рис.15).

1. Три точки, не лежащие на одной прямой L (А,В,С);

 

2. Прямая и точка, не лежащая на данной прямой S(а, C);

 

3. Две пересекающиеся прямые D (ах b);

 

 

4. Две параллельные прямые V ( aII b);

 

 

5. Две проекции отсека плоской фигуры C(АВС).

 

 

Рис.15

 

Задание поверхностей с помощью определителей позволяет просто решать позиционные задачи на принадлежность одних геометрических образов другим.

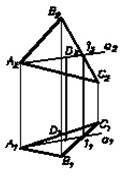
На примере, приведенном на рис.15, решим задачу на принадлежность точки D плоскости C(АВС).

Дано:

C(АВС) –плоскость общего положения;

D(D2) - точка (DÌ C);D1 = ?

Решение:

Дополним чертеж прямой а, которая а Ì C и а2 (А2, D2).

Дальнейший ход решения задачи показан на чертеже.

Из вышесказанного можно сделать вывод, что:

1. точка принадлежит поверхности, если она принадлежит линии, лежащей на данной поверхности;

2. линия принадлежит поверхности, если она отвечает закону образования данной поверхности.

Лекция 3.

 

 

1. Прямая принадлежит плоскости, если минимум две точки этой

прямой принадлежат данной плоскости.

2. Прямая параллельна плоскости, если она параллельна одной из

прямых, принадлежащих данной плоскости. (У прямой, параллельной плоскости, нет общих точек с данной плоскостью).

3. Если прямая и плоскость имеют одну общую точку, то они пересекаются.