Сущность и виды средних величин.

Тема 6. Средние величины в анализе коммерческой деятельности

 

1.Сущность и виды средних величин.

2. Структурные средние величины.

 

Большое распространение в статистике имеют средние величины. В средних величинах отображаются важнейшие показатели товарооборота, цен. Средние величины- это обобщающие показатели, в которых находят выражение действие общих условий, закономерность изучаемого явления.

Важнейшее свойство средней величины заключается в том, что она отражает то общее, что присуще всем единицам исследуемой совокупности.

В практике статистической обработки возникают различные задачи и для их решения требуются различные средние. Виды средней:

средняя арифметическая

средняя геометрическая

средняя гармоническая

средняя квадратическая

средняя кубическая

Какой вид средней выбрать в каждом случае разрешается путем анализа совокупности. Введем понятия и обозначения:

Признак, по которому находится средняя, называется осредненным и обозначается 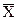; величина осредняемого признака у каждой единицы совокупности называется индивидуальным значением признака или вариантами и обозначается 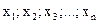; частота – это повторяемость индивидуальных значений признака обозначается f; 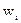=х_i*f_i- объем частот.

Средняя арифметическая наиболее распространенный вид средней. Она исчисляется, когда объем осредняемого признака образуется как сумма его значений:

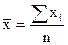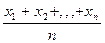= - средняя арифметическая простая

Пример:

Стаж работы: 10 3 5 12 11 7 9

Табельн.

номер рабочего 1 2 3 4 5 6 7

`х= 8,1г.

Часто приходится рассчитывать среднее значение признака по ряду распределения, когда одно и то же значение признака встречается несколько раз. Тогда средняя равна:

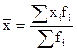- средняя арифметическая взвешенная

Пример:

Заработная плата предприятия

Предриятие	Численность персонала, чел	Месячный фонд зараб.платы	Средняя зараб.плата
Итого			?

 

Определим исходное соотношение средней:

Равна отношению совокупного фонда з/п к общей численности ппп

Допустим, у нас есть данные только граф 1 и 2. Тогда применяется формула средней агрегатной:

=

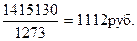
Если мы располагаем только данными граф 1 и 3, тогда применяется средняя арифметическая взвешенная:

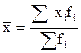
Допустим, в нашем распоряжение есть данные граф 2 и 3, тогда применяется формула средней гармонической:

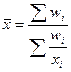- средняя гармоническая взвешенная

Средняя гармоническая применяется тогда, когда статистическая информация не содержит частот по отдельным вариантам, а представлена как их произведение.

В том случае, когда объем явлений, т.е. произведения по каждому признаку равны, применяется невзвешенная средняя гармоническая.

- средняя гармоническая невзвешенная

Средняя невзвешенная используется в тех случаях, когда значения w_i для единиц совокупности равны.

Пример:

2 автомобиля прошли один и тот же путь, один со скоростью 60 км/ч, другой 80 км/ч, средняя скорость составит: