Парушина Н.В.
Кафедра экономического анализа и статистики
Компонентные и топологические уравнения в системах различной природы отражают разные физические свойства, но могут иметь одинаковый формальный вид. Одинаковая форма записи позволяет говорить о формальных аналогиях компонентных и топологических уравнений. Такие аналогии существуют для механических, электрических, гидравлических, пневматических и тепловых объектов.
Наличие таких аналогий приводит к важному следствию: большая часть алгоритмов формирования моделей в САПР могут быть применены к анализу объектов в совершенно различных предметных областях.
Компонентные уравнения имеют вид:
Fк (dV/ dt, V, t) = 0,
а топологические:
Fт (V) = 0,
где V = (v1, v2,…, vn) – вектор фазовых переменных; t – время.
Различают фазовые переменные двух типов:
1) переменные типа потенциала (например, электрическое напряжение);
2) переменные типа потока (например, сила тока).
Каждое компонентное уравнение характеризует связи между разнотипными фазовыми переменными, относящимися к одному компоненту, а топологическое – связи между однотипными фазовыми переменными в разных компонентах.
4. Примеры компонентных и топологических уравнений
Электрические системы. Фазовыми переменными являются электрические напряжения и токи. Компонентами системы могут быть простые двухполюсные элементы и более сложные двух- и многополюсные элементы. К простым двухполюсникам относятся сопротивление, ёмкость и индуктивность R, C и L.
Компонентные уравнения простых двухполюсников:
u = i R; i = C  ; u= L
; u= L ,
,
где u – падение напряжения на элементе, i – ток.
Эти модели лежат в основе моделей других более сложных компонентов. Большая сложность может определяться нелинейностью указанных выше уравнений (т.е. связью R, C и L с фазовыми переменными), или учётом зависимостей R, C и L от температуры, или наличием более двух полюсов. Однако многополюсные компоненты могут быть сведены к совокупности взаимосвязанных более простых элементов.
Топологические уравнения выражают закон Кирхгофа для напряжений (ЗКН) и токов (ЗКТ). Согласно ЗКН, сумма напряжений на компонентах вдоль любого замкнутого контура в эквивалентной схеме равна нулю, а в соответствии с ЗКТ сумма токов в любом замкнутом сечении эквивалентной схемы равна нулю:
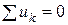 ;
;  .
.
Механические системы. Фазовыми переменными в механических поступательных системах являются силы и скорости. Для составления компонентных и топологических уравнений используют одну из двух возможных электромеханических аналогий. Выберем ту из них, в которой скорость относят к фазовым переменным типа потенциала, а силу считают фазовой переменной типа потока.
Компонентное уравнение, характеризующее инерционные свойства тел, в силу второго закона Ньютона имеет вид
F = M ,
,
где F – сила; M – масса; u – поступательная скорость.
Упругие свойства тел описываются компонентным уравнением, которое получается из закона Гука. В одномерном случае (если рассматриваются продольные деформации упругого стержня)
s = E e,
где s – механическое напряжение, E – модуль упругости, e – относительная деформация, e = /l.
Учитывая, что s = F/S, где S – площадь поперечного сечения тела, и дифференцируя (4), имеем
 или
или  = j u,
= j u,
где j – жёсткость, j = SE/l (величина, обратная жёсткости, – податливость Lм); u – скорость, u = d(Dl)/dt.
Диссипативные свойства в механических системах твёрдых тел выражаются соотношениями, характеризующими связь между силой трения и скоростью взаимного перемещения трущихся тел, причём в этих соотношениях производные сил или скоростей не фигурируют.
Топологические уравнения характеризуют, во-первых, закон равновесия сил: сумма сил, приложенных к телу, включая силу инерции, равна нулю (принцип Даламбера); во-вторых, закон скоростей, согласно которому сумма относительной, переносной и абсолютной скоростей равна нулю.
В механических вращательных системах справедливы компонентные и топологические уравнения поступательных систем с заменой поступательных скоростей на угловые, сил – на моменты вращения, масс – на моменты инерции, жёсткостей – на вращательные жёсткости.
Несмотря на аналогию между электрической и механической системами, имеется и существенное отличие: электрические системы одномерны, а процессы в механическиз часто приходится рассматривать в двух- или трёхмерном пространстве. Следовательно, при моделировании механических систем в общем случае нужно использовать векторное представление фазовых переменных, каждая из которых имеет шесть составляющих.
Гидравлические системы. Фазовыми переменными в гидравлических системах являются расход и давление. Как и для механических систем, компонентные уравнения описывают свойства жидкости рассеивать или накапливать энергию.
Для вывода компонентного уравнения для жидкости на линейном участке трубопровода длиной Dl воспользуемся уравнением Навье-Стокса в следующей его форме (для ламинарного течения жидкости)
 ,
,
где r – плотность жидкости, u – скорость, p – давление, a – коэффициент линеаризованного вязкого трения. Так как u = Q/S, где Q – объёмный расход, S – площадь поперечного сечения трубопровода, то, заменив пространственную производную отношением конечных разностей, получим

или
 ,
,
где Dp – падение давления на рассматриваемом участке трубопровода, Lг – гидравлическая индуктивность, отражающая упругие свойства жидкости, Lг = (Dlr)/S; Rг – гидравлическое сопротивление, отражающее вязкое трение, Rг = 2a/r.
Явление сжимаемости жидкости описывается компонентным уравнением, вытекающим из закона Гука
Dp = E Dl/l.
Дифференцируя (5) и учитывая, что объёмный расход связан со скоростью u = d(Dl)/dt соотношением u = Q/S, получаем
 ,
,
где Cг – гидравлическая ёмкость; Cг = E/(S Dl).
Тема 5. Математическое обеспечение подсистем машинной графики
и геометрического моделирования (МГиГМ)
5.1. Операции обработки данных в подсистемах МГиГМ
Подсистемы машинной графики и геометрического моделирования занимают центральное место в машиностроительных САПР-К. Конструирование изделий в них, как правило, проводится в интерактивном режиме при оперировании геометрическими моделями, т.е. математическими объектами, отображающими форму деталей, состав сборочных узлов и, возможно, некоторые дополнительные параметры (масса, момент инерции, цвета поверхности и т.п.).
В подсистемах МГиГМ типичный маршрут обработки данных включает в себя следующие операции:
– получение проектного решения в прикладной программе;
– представление решения в виде геометрической модели (геометрическое моделирование);
– подготовка проектного решения к визуализации;
– собственно визуализация проектного решения в аппаратуре рабочей станции;
– корректировка решения в интерактивном режиме (при необходимости).
Две последние операции реализуются на базе аппаратных средств машинной графики. Исходя из этого, математическое обеспечение МГиГМ – это, прежде всего, модели, методы и алгоритмы для геометрического моделирования и подготовки проектных данных к визуализации. При этом часто именно математическое обеспечение подготовки к визуализации называют математическим обеспечением машинной графики.
5.2. Классификация моделей геометрических объектов
при трёхмерном моделировании
Различают математическое обеспечение двумерного (2D) и трехмерного (3D) моделирования. Основные применения 2Dграфики – подготовка чертежной документации в машиностроительных САПР, топологическое проектирование печатных плат и кристаллов БИС в САПР радиоэлектронной промышленности.
В большинстве современных машиностроительных САПР используют как 2D, так и 3Dмоделирование при выполнении таких процедур и операций как:
– синтез конструкций;
– представление траекторий рабочих органов станков при обработке заготовок;
– генерация сетки конечных элементов при анализе прочности и т.п.
При трехмерном моделировании различают следующих видов:
1) каркасные (проволочные).
2) поверхностные.
3) объемные (твердотельные).
Каркасная модель представляет форму детали в виде конечного множества линий, лежащих на поверхностях детали. Для каждой линии известны координаты концевых точек и указана их инцидентность (принадлежность) ребрам или поверхностям.
Оперировать каркасной моделью на дальнейших операциях маршрутов проектирования неудобно, и поэтому каркасные модели в настоящее время используют достаточно редко.
Поверхностная модель отображает форму детали с помощью задания ограничивающих ее поверхностей, например, в виде совокупности данных о гранях, ребрах и вершинах поверхности детали.
Особое место среди поверхностных занимают модели деталей с поверхностями сложной формы, так называемыми скульптурными поверхностями. К таким деталям относятся корпуса многих транспортных средств (например, судов, автомобилей), детали, обтекаемые потоками жидкостей и газов (лопатки турбин и насосов, крылья самолетов и др.).
Объемные модели отличаются тем, что в них в явной форме содержатся сведения о принадлежности элементов внутреннему или внешнему по отношению к детали пространству.
5.3. Методы построения геометрических моделей
В настоящее время для построения геометрических моделей применяют следующие методы.
1. Граничный метод; заключается в задании граничных элементов – граней, ребер, вершин.
2. Кинематический метод, согласно которому задают двумерный контур и траекторию его перемещения; след от перемещения контура принимают в качестве поверхности детали.
3. Позиционный метод, в соответствии с которым рассматриваемое пространство разбивают на ячейки (позиции) и деталь задают указанием ячеек, принадлежащих детали; очевидна громоздкость этого подхода.
4. Представление сложной детали в виде совокупностей базовых элементов формы (БЭФ) и выполнения над ними теоретико-множественных операций. К БЭФ относятся заранее разработанные модели простых тел – это, в первую очередь, модели параллелепипеда, цилиндра, сферы, призмы. Типичными теоретико-множественными операциями являются объединение, пересечение, разность. Например, модель плиты с отверстием в ней может быть получена вычитанием цилиндра из параллелепипеда.
Метод на основе БЭФ часто называют методом конструктивной геометрии. Это основной метод конструирования в современных САПР.
В памяти ЭВМ рассмотренные модели обычно хранятся в векторной форме, т.е. в виде координат совокупности точек, задающих элементы модели. Выполнение операций конструирования также выполняется над моделями в векторной форме. Наиболее компактна модель в виде совокупности связанных БЭФ.
Такая модель преимущественно и используется для хранения и обработки информации об изделиях в системах конструктивной геометрии.
Однако для визуализации в современных рабочих станциях в связи с использованием в них растровых дисплеев необходима растеризация – преобразование модели в растровую форму. Обратную операцию перехода к векторной форме, которая характеризуется меньшими затратами памяти, называют векторизацией. В частности, векторизация должна выполняться по отношению к данным, получаемым сканированием изображений в устройствах автоматического ввода графической информации.
5.4. Аналитически описываемые геометрические объекты
Все геометрические объекты можно разделить на две группы:
1. Аналитически описываемые
2. Аналитические неописываемые.
К аналитически описываемым геометрическим объектам (АОГО) относятся: точка, прямая, отрезок, окружность, эллипс, параллелограмм, цилиндр, сфера, эллипсоид, параллелепипед, параболоид и др. К аналитически неописываемым геометрическим объектам (АНГО) относятся объекты, имеющие вид произвольной кривой или неплоской поверхности.
В автоматизированном проектировании наиболее часто использую методы начертательной, аналитической, дифференциальной и проективной геометрии.
5.5. Область применения АНГО
Аналитически неописываемые геометрические объекты используются в следующих отраслях промышленности:
| Отрасль промышленности | Виды технических объектов | Критерии выбора параметров |
| Самолётостроение | Внешний контур самолёта | Аэродинамические свойства |
| Судостроение | Контур судна (обводы), поверхности лопастей корабельных винтов | Гидродинамические свойства |
| Автомобилестроение | Поверхность кузова | Аэродинамические свойства и эстетические требования |
| Энергетическое, химическое, горное машиностроение | Лопасти и другие элементы турбин, лопасти и полости насосов, отводные каналы, реакторные ёмкости | Аэро-, гидро- и термодинамические свойства |
| Инструментальное производство | Рабочие поверхности металло- и деревообрабатывающего инструмента | Прочностные свойства, термодинамические свойства, эффективный отвод стружки |
5.6. Описание аналитически неописываемых геометрических объектов
2-го уровня
5.6.1. Требования к методам описания АН кривых и поверхностей
1. Использование минимума параметров, которые могут быть легко определены.
2. Метод должен допускать локальные и глобальные изменения формы кривых и поверхностей (рис.).
3. Параметры описания должны иметь возможность непрерывно изменяться, даже если кривая имеет кусочно-гладкий вид. Под гладкой дугой понимается дуга кривой с непрерывно изменяющимися касательными.
4. Описание должно обеспечивать возможность определения точек перегиба кривой в случае кривых и точек или кривых пересечения в случае поверхностей.
5. Для описания кривой желательна непрерывность как можно более высокого порядка.
6. В предельном случае метод должен допускать построение прямых линий или плоских поверхностей.
7. Метод должен обеспечивать гладкое соединение кривых или поверхностей.
8. Описание должно предусматривать возможность преобразования и изображения кривых в пространстве.
9. Метод должен предусматривать независимое определение координат произвольной точки объекта.
10. Кривая или поверхность должна быть сегментируемой (кусочно-составной) при сохранении своей исходной формы.
Выполнение этих требований обеспечивается путём использования аппроксимации или интерполяции.
Аппроксимация состоит в определении приближенного описания для исходной кривой или поверхности. Интерполяция – частный случай аппроксимации, в котором требуется согласование исходной и аппроксимирующей кривой в заданных опорных точках.
5.6.2. Аппроксимация кривых с помощью полиномов
Произвольные непрерывные кривые в пространстве можно аппроксимировать аналитически описываемыми объектами: отрезками, дугами окружностей, параболами или кривыми более высокого порядка. Однако применение этих методов ведёт к большим объёмам обрабатываемой информации и требует значительных затрат ресурсов, связанных с разбиением пространственной кривой на отдельные сегменты.
Наиболее известными методами конструирования кривых и поверхностей являются полиномиальная интерполяция Лагранжа и Эрмита. Такой полином для плоской кривой имеет следующий вид:
 ,
,
где ai – коэффициенты полинома; n – порядок полинома.
Если заданы координаты n + 1 точки кривой, то коэффициенты получают как решение системы из n + 1 уравнений.
Преимущества такой аппроксимации:
1. Малая трудоёмкость.
2. Простота вычисления коэффициентов.
Однако такое представление имеет ряд существенных недостатков:
1. Вид аппроксимирующего полинома зависит от выбора системы координат и преобразований над объектом.
2. Зависимость между коэффициентами полинома ai и формой кривой не является очевидной, а выявляется только после соответствующих преобразований. Одному значению параметра может соответствовать несколько значений зависимых переменных.
Указанные недостатки характерны также и для пространственных кривых и поверхностей. Вследствие этого обычно используют не явные (канонические), а параметрические формы представления объектов.
5.6.3. Параметрическое описание кривой в форме Фергюсона
Параметрическое задание пространственной кривой имеет следующий вид:
x = x(u); y = y(u); z = z(u),
где u Î I; I – интервал описания.
Каждому значению параметра u соответствует одно значение зависимых переменных. При этом каждая переменная изменяется независимо от других. Выбор системы координат не влияет на форму кривой.
Для описания кривых обычно используются методы кусочно-линейной аппроксимации полиномами, заданными в параметрической форме. При выборе конкретного метода из множества возможных необходимо выполнить ряд требований:
1. Методы должны обеспечивать гладкое соединение отдельных кривых (сегментов поверхностей)
2. Методы должны обеспечивать возможность управления формой кривой путём изменения небольшого количества параметров.
3. Включение нового сегмента кривой не должно нарушать гладкость всей кривой.
Перечисленным требованиям удовлетворяет, например, кривая в форме Фергюсона. Плоская кривая в этой форме описывается уравнением вида:
P(u) = mu3 +nu2 + pu + q,
где u – параметр;
m, n, p, q – постоянные коэффициенты.
Значения коэффициентов определяются из следующих предположений:
– значение параметра u в начальной точке кривой равно 0; а в конечной точке – 1;
– известны координаты граничных точек кривой P(0) и P(1), а также значения производной в этих точках.
С учётом этих предположений величины m, n, p, q находятся из решения следующей системы уравнений:

Решив эту систему, получаем:
m = 2 (A – B) + C + D;
n = 3 (B – A) – 2C – D;
p = C;
q = A.
Параметрическая кривая, заданная в форме Фергюсона, имеет следующие свойства:
1. Кривая полностью определена условиями, заданными в граничных точках.
2. Касательные к кривой, проведенные в граничных точках, параллельны векторам производной. Поэтому возможно гладкое соединение сегментов кривых, если равны координаты их граничных точек.
3. Изменение модулей векторов производных приводит к изменению формы кривой.
5.6.4. Определение кубических сплайн-функций
Функция, которая составлена из полиномов k-й степени и в узлах является (k – 1) раз непрерывно дифференцируемой, называется сплайн-функцией. Если заданы также опорные точки, через которые проходит кривая, описываемая этой функцией, то она называется интерполирующей сплайн-функцией или сплайном.
Функция Q(u) называется кубическим сплайном, если она удовлетворяет следующим условиям:
1. Задан упорядоченный набор из n + 1 точки u0,…, un (узлы сплайна) и соответствующие узлам опорные точки S0,…, Sn.
2. На каждом интервале (uk, uk–1) для k = 0, 1, 2,…n – 1 функция Q(u) является кубическим полиномом fk(u) (k =3):
fk(u) = Ak(u – uk)3 + Bk(u – uk)2 + Ck(u – uk) + Dk.
3. В узлах u0,…, un функция принимает заданные значения S0,…, Sn:
Q(uk) = Sk, k = 0, 1, 2,…n.
4. На всём интервале, включая и узлы, Q(u) должна быть дважды непрерывно дифференцируемой функцией:
fk¢ (uk) = fk + 1¢ (uk),
fk¢¢ (uk) = fk + 1¢¢ (uk).
5. Заданы значения первых производных в граничных точках u0 и un или значения первых двух производных в граничной точке u0.
Преимущества кубических сплайнов:
1. Удобство использования, так как для построения кривой необходимы только значения сплайн-функции в узлах (опорные точки) и значения первых производных в концевых точках.
2. На каждом интервале кривая определяется кубическим полиномом.
3. Так как кривая на всем интервале дважды непрерывно дифференцируема, то у неё нет точек перегиба.
5.6.5. Представление пространственной кривой по Эрмиту
Для конструирования пространственной кривой с использованием интерполяционных полиномов Эрмита необходима геометрическая информация о концевых точках кривой и задание первых n производных в этих точках. Для интерполяции кривой на заданном интервале используются кубические полиномы следующего вида:
x(u) = axu3 + bxu2 + cxu + dx;
y(u) = ayu3 + byu2 + cyu + dy;
z(u) = azu3 + bzu2 + czu + dz.
При определении коэффициентов ax, bx, cx, dx с использованием координат концевых точек, а также концевых касательных векторов получаем представление кривой в матричной форме:
 ,
,
где U – матрица-вектор степеней параметра, U = (u3, u2, u, 1);
MH – матрица Эрмита:
 ;
;
GH – вектор координат концевых точек кривой:
 ;
;
P(0), P(1) – координаты концевых точек кривой.
Желаемую форму кривой можно получить при изменении длины касательных векторов или их направления.
Интерполяция пространственной кривой по Эрмиту позволяет построить гладкую кривую, но для получения её желаемой формы необходимо относительно плотно установить опорные точки (концевые точки сегментов).
5.6.6. Представление кривой по Безье
Кривая в форме Безье аппроксимирует ломаную, вершинами которой являются опорные точки (рис.). Эту ломаную называют характеристической ломаной заданной кривой. Граничные точки кривой Безье совпадают с крайними вершинами характеристической ломаной, причём первое и последнее звенья ломаной являются касательными к кривой соответственно в начальной и конечной точках. Форма кривой Безье зависит от расположения вершин характеристической ломаной.
Представление кривой Безье в матричной форме имеет вид:
 ,
,
где MB – матрица Безье:
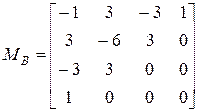 ;
;
GB – вектор координат концевых точек кривой, GB = GH.
Достаточным условием гладкости соединения двух кривых Безье является равенство в концевых точках соединяемых сегментов касательных векторов этих сегментов.
Недостатком параметрического представления кривой по Безье является тот факт, что степень кривой растёт пропорционально количеству звеньев характеристической ломаной, а изменение вершин ломаной влияет на всю форму кривой.
5.6.7. Представление кривой с помощью B-сплайнов
Пусть U = (u0 = 0, u1, …, ui, un = n) – разбиение интервала [0, n] на отрезки, где ui = i, а i = 0 … n – натуральное число. Точки ui называются узлами, U – множеством узлов. B-сплайном k-го порядка называется функция Mi,k(x), равная нулю на данном множестве узлов, за исключением последовательных отрезков.
В случае B-сплайнов аппроксимируемая кривая делится на n участков ,
выделяемых последовательными точками P0, P1, P2,…Pn. Участок между парой соседних точек Pi и Pi+1 аппроксимируется B-сплайном, построенным с использованием четырех точек Pi–1, Pi, Pi+1 , Pi+2. Аппроксимация с помощью B-сплайнов позволяет получить кривые, которые имеют такие же свойств, как и кривые Безье.
Представление кривой с помощью B-сплайнов в матричной форме имеет вид:
 ,
,
где MBS – матрица B-сплайнов:
 ;
;
GBS – вектор координат узлов:
 .
.
В случае построения кривых методом B-сплайнов необходимо иметь зависимость между опорными точками кривой Pi и узлами ui.
Свойства кривой, построенной с использованием B-сплайнов:
1. Кривая определяется линейной комбинацией сплайн-функций.
2. Локальное изменение опорных точек не приводит к изменению всей формы кривой.
3. Кривая может содержать прямолинейные отрезки.
5.7. Описание аналитически неописываемых геометрических объектов
3-го уровня
5.7.1. Описание поверхности по Фергюсону
Кривая в форме Фергюсона определяется координатами концевых точек и значениями производных в них. Если такие четыре кривые замкнуть, то полученный контур можно рассматривать как границу участка (отсека) поверхности.
Внутренняя часть поверхности также определяется с помощью кривых в форме Фергюсона, которые в зависимости от параметров соединяют две противолежащие границы отсека (рис.). Границы отсека сами задают концевые точки переменной кривой. Например, кривы AB и DC определяют концевые точки кривой EF, которая изменяется в направлении параметра u.
5.7.2. Описание поверхности методом Кунса
Поверхность в трёхмерном пространстве определяется множеством точек, которые имеют две степени свободы. Если u и v – два независимых параметра, то поверхность, построенная методом Кунса, определяется следующим образом:
(x, y, z) = (X(u, v), Y(u, v), Z(u, v)).
Независимые переменные u и v изменяются в интервале от 0 до 1. Соответственно, границы описываемого отсека поверхности:
P(u, v) = uv;
P(u, 0) = u0;
P(u, 1) = u1;
P(0, v) = 0v;
P(1, v) = 1v.
где P(u, v) – функция двух переменных.
Зафиксировав два параметра, можно определить точку на поверхности. Так определяются концевые точки отсека поверхности. Для дальнейшего описания поверхности Кунс ввёл скалярные функции смешения, являющиеся функцией одной переменной.
Если граница отсека поверхности описывается полиномом третьей степени, то при его записи в параметрической форме функции смешения имеют следующий вид:
F0 (u) = F0u = 2u3 – 3u2 + 1;
F1 (u) = F1u = – 2u3 + 3u2;
G0 (u) = G0u = u3 – 2u2 + u;
G1 (u) = G1u = u3 – u2.
Уравнение для бикубического участка поверхности в матричной форме имеет вид:
Q(u, v) = (F0u, F1u, G0u, G1u)·P·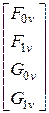 ,
,
где P – матрица, содержащая значения векторов, характеризующих положение границ поверхности, и значения векторов производных в углах участков поверхности.
5.7.3. Описание поверхности по Безье
Поверхность, построенная по методу Безье, определяется множеством точек, которые образуют характеристическую сетку (рис.). Такие точки поверхности называются вспомогательными. Если этим точкам приписать двойной индекс, то их можно рассматривать как элементы матрицы. В этом случае задача конструирования поверхности сводится к определению поверхности по заданной характеристической сетке.
Пусть задана матрица размером (m, n), элементы которой образуют характеристическую сетку. Из матрицы выбираются все элементы с одинаковым первым индексом, т.е. элементы одной строки. Через вспомогательные точки, которые соответствуют этим элементам, проводится характеристическая ломаная. В результате образуются m характеристических ломаных и, соответственно, определены m кривых Безье. На каждой кривой находится точка, которая соответствует которая соответствует определённому значению параметра u. Через полученные m точек проводится новая характеристическая ломаная, определяющая кривую Безье с постоянным значением параметра u. Для любого заданного значения параметра v на этой кривой находится искомая точка поверхности P(u, v).
5.7.4. Описание поверхности методом B-сплайнов
Определение поверхности методом B-сплайнов аналогично определению поверхности по Безье для случая, когда степень B-сплайн-функций соответствует количеству опорных точек.
Наиболее удобен метод аппроксимации поверхности кубическими B-сплайнами.
Тема 6. Автоматизация конструкторского проектирования
6.1. Классификация задач конструкторского проектирования
Основная цель конструкторского проектирования – реализация принципиальных схем, полученных на этапе функционального проектирования. При этом производятся конструирование отдельных деталей, компоновка узлов из деталей и конструктивных элементов, агрегатов из узлов, после чего оформляется техническая документация на объект проектирования.
Задачи конструкторского проектирования делятся на две группы:
1. Определение геометрических параметров конструкции – геометрическое проектирование.
2. Синтезирование структуры (топологии) конструкции с учётом её функциональных характеристик – топологическое проектирование.

Классификация задач конструкторского проектирования показана на рис. 6.1.
Рис. 6.1. Классификация задач конструкторского проектирования
6.2. Задачи геометрического проектирования
6.2.1. Задачи геометрического синтеза
Задача синтеза геометрических объектов (ГО) состоит в формировании сложных ГО из элементарных ГО заданной структуры. Такая задача возникает, например, при оформлении деталировочных чертежей.
Основным критерием геометрического синтеза является точность воспроизведения требуемой формы ГО.
Решение задачи синтеза формы (облика) изделия обеспечивает получение оптимальной или рациональной формы деталей, узлов или агрегатов, влияющей на качество функционирования объекта проектирования. Такие задачи возникают на ранних стадиях проектирования, например, при определении конфигурации корпуса судна, автомобиля, летательного аппарата и т.д. Часто встречаются задачи этой группы, связанные с синтезом формы корпусов узлов с учётом максимальной теплоотдачи (корпуса электродвигателей).
6.2.2. Задачи геометрического моделирования
К типовым позиционным задачам относят:
– определение принадлежности точки к плоской области, ограниченной замкнутыми контурами;
– определение координат точки пересечения прямой с криволинейным контуром или поверхностью;
– установление факта пересечения контуров и вычисление координат их точек пересечения;
– определение взаимного расположения плоских или пространственных областей.
На основе типовых позиционных решаются следующие конструкторские задачи:
– определение факта касания или столкновения движущихся деталей;
– определение факта наложения деталей;
– проверка гарантированных зазоров между деталями;
– оценка погрешности обработки контуров и поверхностей деталей на станках с ЧПУ.
К метрическим задачам относят:
– вычисление длины отрезка;
– вычисление периметра и площади плоских и пространственных областей;
– определение центра масс плоских контуров и объёмных тел;
– определение массы, моментов инерции и моментов сопротивления;
– определение напряжений и деформаций.
6.2.3. Задачи оформления конструкторской документации
В текстовой конструкторской документации содержатся:
– описательная часть (служебное назначение изделия);
– характеристики и паспортные данные узлов и агрегатов;
– ТУ на изготовление, сборку, наладку и эксплуатацию изделий;
– спецификации и экспликации.
К графической конструкторской документации относятся:
– деталировочные и сборочные чертежи;
– схемы структурные, функциональные и принципиальные (электрические, электронные, пневматические, гидравлические и др.);
– графики структурных сеток кинематических цепей;
– циклограммы и зависимости для выбора параметров режимов работы агрегатов и устройств.
6.3. Задачи топологического проектирования
6.3.1. Задачи топологического синтеза
Решение задачи компоновки состоит в формировании конструктивных элементов высшего иерархического уровня из элементов низшего иерархического уровня. Это наиболее трудоёмкая часть конструкторского проектирования.
Задача компоновки машиностроительных узлов и систем обычно состоит из двух частей: эскизной и рабочей. При решении эскизной части задачи компоновки по функциональной схеме разрабатывают общий вид конструкции узла. На основе эскизной компоновки решают задачу рабочей компоновки, т.е. составляют рабочую компоновку узла или агрегата с более детальной проработкой конструкции.
Например, процесс компоновки зубчатого редуктора выполняется по его кинематической схеме. Эскизная компоновка редуктора разрабатывается после расчёта передаточных чисел ступеней. Рабочая компоновка заключается в установке в редуктор спроектированных валов и зубчатых колёс, обеспечивающих заданные передаточные отношения, подшипников, уплотнений и других конструктивных элементов. Критериями компоновки редуктора могут быть его масса, габаритные размеры, удобство ремонта и обслуживания и др.
Другие разновидности задачи компоновки и остальные типы задач топологического синтеза в наибольшей степени формализованы при конструировании электронной аппаратуры.
Задача покрытия заключается в преобразовании функциональной схемы соединений логических элементов электронного узла в схему соединений типовых конструктивных элементов (модулей). Критериями качества при решении задачи покрытия могут быть суммарная стоимость и общее количество модулей, количество типов используемых модулей, количество связей между модулями, общее количество неиспользованных логических элементов в модулях и др.
При решении задачи разбиения осуществляется разделение схемы соединений конструктивных элементов на конструктивно обособленные части (узлы) на некотором иерархическом уровне. Основными критериями качества при решении задачи разбиения являются: длина внешних связей, характеризуемая или количеством межузловых соединений, или количеством внешних выводов всех узлов, количество образующихся узлов, количество различных типов узлов.
Типичной задачей размещения в проектировании электронных устройств является определение оптимального пространственного расположения элементов на заданной поверхности (коммутационном поле). Критерии и ограничения при решении задачи размещения можно разделить на метрические и топологические. К метрическим относятся: размеры элементов и расстояния между ними, размеры коммутационного поля, расстояния между выводами элементов, допустимые длины соединений; к топологическим – количество пространственных пересечений соединений, количество межслойных переходов, близость расположения друг к другу тепловыделяющих элементов или электромагнитно несовместимых элементов и соединений. Если связи между соединениями осуществляются проводным монтажом, то основным критерием оптимальности решения задачи размещения является суммарная взвешенная длина соединений.
Задача трассировки заключается в определении геометрии соединений конструктивных элементов электронных устройств. Различают три вида трассировки: проводных, печатных и пленочных соединений. Критериями оптимальности решения задачи трассировки могут быть: минимальная суммарная длина соединений, минимальное количество слоев монтажа, минимальное количество переходов из слоя в слой, минимальные наводки в цепях связи элементов и т.д.
С решением задач размещения и трассировки сталкиваются не только при проектировании радиоэлектронных устройств, но и при проектировании объектов других отраслей техники: при размещении технологического оборудования в цехе, размещении элементов гидросистемы станка, трассировке транспортных потоков в цехе, прокладке нефте-, газо- и продуктопроводов, прокладке дорог и т.д.
6.4. Математические модели задач топологического проектирования
6.4.1. Метод проб и ошибок. Эвристические приёмы
Основным традиционным методом, которым пользуется конструктор в процессе получения технических решений, является метод проб и ошибок. Суть этого метода заключается в том, что на первом этапе формулируется исходное предложение (гипотеза), по разрабатываемой конструкции в виде её схемы или эскиза. Конструктор лишь интуитивно предполагает, что данный вариант окажется работоспособным. На втором этапе проверяется (с помощью моделирования или экспериментальных исследований) качество предложенного варианта. Обычно после первой пробы не удаётся получить требуемое проектное решение. Тогда формируется второе предложение, которое учитывает ошибки, допущенные в первом предложении и т.д.
Метод проб и ошибок часто используется следующим образом: задаются каким-либо значением неизвестного конструктивного параметра, а затем в результате вычислений других конструктивных параметров оценивают приемлемость принятого значения первого параметра. Эту процедуру повторяют до тех пор, пока не будет найдена совокупность значений конструктивных параметров, соответствующих ограничениям на параметры и качественным показателям конструкции.
Основой для формирования проектных гипотез обычно служит базовая модель, т.е. действующий образец конструкции машины или отдельного узла.
Повышение эффективности поиска новых конструктивных решений обеспечивается применением эвристических приемов изобретательской деятельности: инверсии, аналогии, метода "мозгового штурма" и др.
Инверсия предполагает изменение на обратные каких-либо функций, форм, способов расположения деталей конструкции.
В результате инвертирования конструкция по сравнению с исходной может приобрести новые эксплуатационные и технологические свойства.
Аналогия опирается на подобие конструкций в природе и технике. Аналогия широко применятся в робототехнике при разработке механических устройств роботов и их органов чувств.
Метод "мозгового штурма" – метод коллективного генерирования технических решений.