Первичная обработка статистического материала.
Раздел I.
Исходный материал для камеральной работы находится в табл. 1(приложение «Данные измерений диаметров и высот деревьев»). Таблица содержит 205 пар измерений диаметра и соответствующей ему высоты.
Общее содержание этой таблицы в статистике определяется как результаты наблюдения (измерения, испытания, эксперимента). Сам процесс сбора данных называется статистическим наблюдением, которое может быть как простой визуальной оценкой изучаемого явления, так и достаточно сложным экспериментом с целью получения характеристики исследуемого признака. Этап статистического наблюдения – важная работа, от нее зависит корректность результатов всего эксперимента и она требует соответствующей математической подготовки экспериментатора. Именно поэтому этап наблюдения пропущен, студент начинает знакомство со статистикой на базе уже выполненного статистического наблюдения.
Обычно, студент использует в камеральной работе 100-150 пар значений диаметра и высоты. В терминах статистики диаметр и высота – это изучаемые признаки. То есть по каждому признаку контрольная работа содержит, допустим, 100 единиц измерений диаметра(d), и, соответственно 100 единиц измерений высоты(h). Этот объем измерений как по диаметру, так и по высоте называется выборкой, т.е частью от большой совокупности. Таким образом, имеется выборка по диаметру объемом 100 едениц и выборка по высоте с таким же объемом.
Конечной целью контрольной работы (КР) является установление количественной меры связи двух изучаемых признаков – диаметра и высоты (иногда говорят о построении модели связи). Зависимость высоты от диаметра, также как и обратная зависимость -диаметра от высоты естественна и ее оценка очевидна. Однако, количественно эта зависимость может быть описана только методами математической статистики. В рамках очевидной тенденции они дают ответ на вопрос: в какой мере в общем объеме выборки, высота определяется изменением диаметра, а также на сколько единиц изменяется высота при изменении диаметра на одну единицу.
При визуальной попарной оценке двух признаков можно найти подтверждение очевидному: чем больше диаметр, тем больше высота. Однако для того, чтобы количественно оценить эту зависимость, необходимо подвергнуть каждую выборку (по диаметру и по высоте) специальным этапам обработки.
Первым этапом обработки является процедура построения вариационных рядов. Построение вариационного ряда преследует две цели: 1) вскрыть закономерности, которым следует распределение изучаемого признака, т.е. установить какие значения и как часто встречаются в объеме выборки; 2) упростить исходную информацию за счет группировки данных. Группировка материала достигается путем разбиения полного диапазона изменения значений признака ( Xmax – Xmin ), который называется размахом вариации, на определенное количество интервалов. Величина интервала (К) устанавливается по формуле Стерджесса:
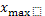– максимальное значение признака.
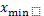– минимальное значение признака.
N – объем выборки, который стоит под знаком десятичного логарифма.
Если число, обозначающее величину интервала получилось дробным, его округляют до целого значения.
Рассмотрим пример.
Допутим произведено измерение диаметров на высоте груди у пятидесяти деревьев, т.е объем выборки по диаметру составляет 50едениц.
Результаты измерений с точностью до 0,1см.
Исходные данные по высоте и диаметру.
| № | Диаметр | Высота | № | Диаметр | Высота |
| 7,7 | 8,3 | 29,0 | 21,8 | ||
| 12,4 | 8,8 | 14,1 | 16,2 | ||
| 14,3 | 11,4 | 13,0 | 16,0 | ||
| 20,2 | 19,0 | 15,0 | 17,9 | ||
| 23,7 | 21,5 | 17,8 | 20,5 | ||
| 24,9 | 22,3 | 14,2 | 15,0 | ||
| 28,2 | 22,6 | 18,2 | 19,5 | ||
| 30,7 | 22,5 | 21,4 | 21,3 | ||
| 6,4 | 7,9 | 22,1 | 21,5 | ||
| 11,8 | 14,8 | 12,7 | 16,8 | ||
| 9,5 | 11,4 | 17,5 | 17,7 | ||
| 12,8 | 12,9 | 14,8 | 16,8 | ||
| 15,8 | 18,2 | 21,2 | 15,2 | ||
| 16,4 | 19,2 | 12,5 | 15,5 | ||
| 17,2 | 19,6 | 22,9 | 20,4 | ||
| 20,8 | 22,7 | 11,5 | 12,7 | ||
| 21,1 | 20,0 | 17,0 | 17,4 | ||
| 22,8 | 20,9 | 15,3 | 17,4 | ||
| 18,5 | 20,7 | 16,5 | 19,5 | ||
| 25,2 | 23,2 | 20,5 | 21,5 | ||
| 26,7 | 21,8 | 19,1 | 17,4 | ||
| 33,8 | 25,7 | 15,7 | 18,5 | ||
| 10,2 | 9,5 | 17,2 | 20,7 | ||
| 16,3 | 17,8 | 19,7 | 16,8 | ||
| 23,1 | 21,5 | 19,9 | 22,7 |
Находим в этой выборке минимальный и максимальный диаметры. Они равны соответственно 6,4 и 33,8 см.
Рассчитаем величину интервала, приемлемую для данной выборки:
Приступаем к построению вариационного ряда по следующим правилам:
1) Минимальное значение признака должно попадать в первый интервал.
2) Срединное значение интервала должно быть кратно его величине.
Строим первый интервал, ориентируясь на Xmin. Ближайшее к нему число кратное величине интервала (4см) – 8. Значит 8см – является срединным значением интервала при его вычисленной величине 4см. Тогда нижняя граница первого интервала будет равна 6см, а верхняя 10см. Таким образом, по приведенным выше правилам мы построим первый интервал вариационного ряда: 6,0 – 10,0. Прибавляя последовательно к нижней и верхней границе по 4см (величина интервала) получаем границы последующих интервалов: 10,0 – 14,0; 14,0 – 18,0; 18,0 – 22,0 и т.д.
Для того, чтобы избежать перекрытия верхних границ предыдущего интервала с нижними границами последующего допустимо добавить ко всем нижним границам интервал 0,1, как значение точности измерения признака. Тогда в окончательном виде вариационный ряд будет выглядеть следующим образом: