Анализ общего риска: активы, рассматриваемые изолированно

Понятия распределения вероятностей и ожидаемой величины могут исполь­зоваться как основа для измерения риска. Известно, что риск присутствует в том случае, если исследуемые распределения имеют более одного возможного ис­хода, однако каким образом можно измерить риск и оценить его количественно? Чтобы ответить на этот вопрос, рассмотрим сначала методику исчисления об­щего риска.

Выше мы предположили, что возможны 5 состояний экономики (см. табл. 3.1). На самом же деле состояние экономики может варьироваться от самой глубокой депрессии до наивысше­го подъема с бесчисленным количеством промежуточных поло­жений. Обычно среднему (нормальному) состоянию соответству­ет самая большая вероятность, далее значения вероятностей рав­номерно уменьшаются при удалении от нормы как в одну (подъ­ем), так и в другую (спад) сторону, стремясь к нулю в крайних по­ложениях (полная депрессия и наибольший подъем). Если при этом величина доходности, соответствующая нормальному поло­жению, является одновременно и средним арифметическим двух крайних значений, то мы получаем распределение, которое в тео­рии вероятностей носит название «нормального». Его графическое изображение дано на рис. 3.2.

Нормальное распределение достаточно полно отражает реаль­ную ситуацию и дает возможность, используя ограниченную ин­формацию, получать числовые характеристики, необходимые для оценки степени риска того или иного проекта. Далее будем всегда предполагать, что мы находимся в условиях нормального распре­деления вероятностей.

Замечание.В действительности в чистом виде нормальное распределение в экономических явлениях встречается редко, однако, если однородность совокупности соблюдена, часто фактические распределения близки к нормальному.

 

Вопрос 2.Реальные распределения вероятностей могут существенно отличаться от нормального. Насколько сильно будут искажены наши выводы, если в наших рассуждениях мы будем исходить только из нормального закона распределения вероятностей?

Ответ: а) затрудняюсь ответить; б) существенно искажены; в) искажения будут несущественными.

Правильный ответ в).

При любом варианте ответа см. справку 2.

 

Справка 2. Даже если распределение не является близким к нормальному, на основании тео­ремы Чебышева можно утверждать, что для любого распределения не менее 89% всех исходов лежит в пределах трех средних квадратических отклонений от ожидаемого значения.

 

 

ERR

Рис. 3.2. Нормальное распределение вероятностей

 

На рисунке 3.1 приведены графики распределения вероятностей для проектов 1 и 2. Условиям нормального распределения удовлетворяет проект 2.

Для большей прозрачности дальнейших рассуждений, полезно предварительно решить самостоятельно следующую задачу

 

Задача 1. Рассмотрим два финансовых проекта А и В, для кото­рых возможные нормы доходности (IRR ) находятся в зависимо­сти от будущего состояния экономики. Данная зависимость отра­жена в таблице 3.2

Таблица 3.2.

Данные для расчета ожидаемой нормы доходности вариантов вложения капитала в проекты А и В

Состояние экономики	Вероятность данного состояния	Проект А, IRR	Проект В, IRR
Подъем Норма Спад	P1 = 0,25 Р2 = 0,5 Р3 = 0,25	90% 20% - 50%	25% 20% 15%

Рассчитайте для каждого из проектов ожидае­мую норму доходности ERR.Сравните результаты своих вычислений с ответом.

Ответ: Для проекта А по формуле (3.1) получаем:

ERR_А = 0,25 ´ 90% + 0,5 ´ 20% + 0,25 ´ (-50%) = 20%.

Для проекта В:

ERR_В = 0,25 ´ 25% + 0,5 ´ 20% + 0,25 ´ 15% = 20%

 

Таким образом, для двух рассматриваемых проектов ожидае­мые нормы доходности совпадают, несмотря на то, что диапазон возможных значений IRR сильно различается: у проекта А от -50% до 90%, у проекта В от 15% до 25%. На рисунке 3.3 приведены графики распределения вероятностей для проектов А и В, (они удовлетворяют условиям нормального распределения).

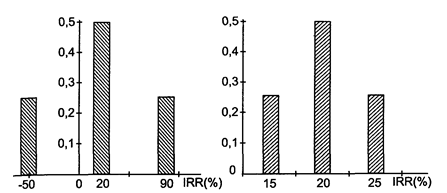
Рис. 3.3. Распределение вероятностей для проектов А и В

Предполагается, что для проекта А в наихудшем случае убыток не составит более 50%, а в наилучшем случае доход не превысит 90%. Для проекта В 15% и 25% соответственно. Очевидно, что тогда значение ERR останется прежним (20%) для обоих проектов, совпадая со значением среднего состояния. Со­ответствующая же среднему значению вероятность понизится, причем не одинаково в наших двух случаях.

	р

ERR

 

 

Рис. 3.4. Распределение вероятностей для проектов А и В

Очевидно, чем более «сжат» график, тем выше вероятность, со­ответствующая среднему ожидаемому доходу (ERR), и вероят­ность того, что величина реальной доходности окажется доста­точно близкой к ERR. Тем ниже будет и риск, связанный с соот­ветствующим проектом. Поэтому меру «сжатости» графика мож­но принять за достаточно корректную меру риска.

Меру «сжатости» определяет величина, которая в теории веро­ятности носит название«среднеквадратичного отклонения» - s - и рассчитывается по следующей формуле

(3.2)

Чем меньше величина s, тем больше «сжато» соответствующее распределение вероятностей, и тем менее рискован проект. При этом для нормального распределения вероятность «попадания» в пределы ERR ± s составляет 68,26%.

Рассчитаем значение s для рассматриваемых проектов А и В.

Проект А:

%

Проект В:

%

Как видим, для второго проекта с вероятностью 68,26% можно ожидать величину доходности IRR = 20% ± 3,5%, т.е. от 16,5% до 23,5%. Риск здесь минимальный. Проект А гораздо более риско­ванный. С вероятностью 68,26% можно получить доходность от -29,5% до 69,5%. Считается, что среднерискованной операции соответствует значение s около 30%.

В рассмотренном примере распределение вероятностей пред­полагалось известным заранее. Во многих ситуациях бывают дос­тупны лишь данные о том, какой доход приносила некая финан­совая или хозяйственная операция в предыдущие годы.

С позиции развиваемых представлений проанализируем рассмотренный в самом начале темы пример 1.

Рассчитаем, например, дисперсию доходности проекта 2 по данным табл. 3.1. Нам известно, что ожидаемая доходность проекта, равна 12.0%. Следовательно, дисперсия равна

= (-2,0 – 12,0)²0,05 + (9,0 – 12,0)²0,20 + (12,0-12,0)²0,50 +

+(15,0-12,0)²0,20 + (26,0-12,0)²0,05 = 23,20,

а среднее квадратическое отклонение доходности проекта 2 – s =4,82%

Используя этот показатель в качестве меры разброса, можно сделать ряд полез­ных выводов о распределении исходов. В частности, если распределение явля­ется непрерывным и близким к нормальному, можно утверждать, что 68.3% всех исходов лежит в пределах одного среднего квадратического отклонения от ожидаемого значения, 95.4% — в пределах двух средних квадратических отклонений и практически все исходы (99.7%) — в пределах трех средних ква­дратических отклонений.

В табл. 3.3 приводятся ожидаемые значения доходности, дисперсия и сред­нее квадратическое отклонение по всем четырем альтернативным вариантам ин­вестирования примера 1, а также коэффициент вариации, который мы рассмотрим в сле­дующем разделе. Мы видим, что ГКО-ОФЗ обладают наименьшими значениями показателей дисперсии и среднего квадратического отклонения, а проекту 2 соответствуют наибольшие их значения.

По данным табл. 3.3 можно, казалось бы, прийти к заключению, что казна­чейские векселя — наименее рисковый вариант инвестирования, а проект 2 — наиболее рисковый. Однако это не всегда верно; перед тем как сделать оконча­тельный вывод, необходимо принять во внимание ряд других факторов, таких как численные значения ожидаемой доходности, асимметрия распределения, до­стоверность наших оценок распределения вероятностей и взаимосвязь каждого актива с другими активами, включенными в портфель инвестиций.