Какик показатели качества регулирования имеют первостепенное значение? Приведите примеры.

Контрольные вопросы.

Рис.5.81. Кривой D – разбиения

Рис.5.80.Построение кривой D – разбиения

Рис.5.79.Кривая D – разбиения 1 и особые прямые 2 т 3.

Рис.5.78.Логарифмические амплитудные и фазовые характеристики

Рис.5.77.АФХ для выяснения правил применения критерия Найквиста к логарифмическим характеристикам

Рис.5.75. АФХ

Рис.5.74.К выводу критерия устойчивости Найквиста для случая неустойчивых систем в разомкнутом состоянии

Рис.5.71.Годографы типовых звеньев

Рис.5.70. Построение годографа системы по годографам звеньев

Рис.5.68.Годограф Михайлова

Рис.5.65.Схема к выводу принципа аргумента

Рис.5.64.Расположение корней характеристического уравнения на комплексной плоскости

Рис.5.63.Кривые изменения регулируемого параметра при регулировании

Раздел 5. Лекция 5. Устойчивость процесса автоматического управления

Условиями работоспособности САР (САУ) являются её устойчивость и обеспечение необходимого качества регулирования (управления). Устойчивость конкретной системы с заданным ТОУ и выбранным регулятором определяется на основе критериев устойчивости или путём моделирования. Анализ устойчивости является первым этапом исследования системы и выполняется обычно для вновь проектируемых САР (САУ), динамические свойства которых недостаточно изучены.

Для хорошо изученных САР (САУ) анализ устойчивости исключается, если заранее известно, что эти системы принадлежат к классу устойчивых. В таких случаях анализ работоспособности системы исчерпывается определением качества регулирования (управления).

Рис.5.59.Показатели качества регулирования: 1-кривая разгона; 2-процесс регулирования при нанесении возмущения при нагрузке; 3-процесс регулирования при нанесении возмущения по заданию без статической ошибки; 4-процесс регулирования при нанесении возмущения по заданию со статической ошибкой

Основные показатели качества регулирования приведены на рис.5.59, ими являются:

1.Статическая ошибка или остаточное отклонение - это отклонение регулируемой величины от заданного значения, которое остаётся после окончания процесса регулирования. Кривая 4 на рис.3.15 соответствует процессу регулированию при возмущении по заданию. Первоначальное заданное значение регулируемой величины в момент было изменено на . Остаточное отклонение характерно для регулирующих устройств пропорционального действия.

2.Максимальное динамическое отклонение 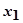, равное первому выбегу регулируемой величины, обычно бывает максимальным. Оно зависит от динамических свойств объекта, вида возмущения, закона регулирования и настроек регулирующего устройства (регулятора).

Степень воздействия регулятора на отклонение регулируемой величины при нанесении возмущения оценивается динамическим коэффициентом регулирования R_д, который статических объектов равен:

где 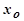- отклонение регулируемой величины при внесении равноценного возмущения и при отсутствии регулятора; - коэффициент передачи объекта; - возмущение.

Для астатических объектов, не обладающих свойств самовыравнивания, установившиеся значения 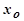отсутствует и динамический коэффициент регулирования определяется выражением , - ступенчатое возмущение; - запаздывание астатического объекта; - условная постоянная времени астатического объекта.

3.Перерегулирование - это отношение амплитуд двух последующих выбегов регулируемой величины при возмущении по заданию, которое характеризует Колебательность переходного процесса при регулировании: ,

или отношения амплитуды первого выбега к изменению задания при возмущении по заданию .

Очевидно, что в случае возмущения по нагрузке при апериодическом процессе регулирования; при колебательном затухающем переходном процессе; при колебательном незатухающем процессе; 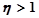при расходящихся колебаниях.

Величина перерегулирования зависит от динамических свойств ТОУ и регулятора, т.е. от закона регулирования и настроек регулятора.

4.Время регулирования , численное равное продолжительности переходного процесса, т.е. времени от момента внесения возмущения, приводящего к отклонению регулируемой величины от задания, до её возвращения к заданному значению с точностью, определяемой зоной нечувствительности измерительного и регулирующего комплектов аппаратуры.

Время регулирования зависит от динамических свойств объекта, закона регулирования и настроек регулятора. Однако оно не может быть меньше некоторого минимального значения, зависящего в первую очередь от динамических свойств объекта.

5.Интегральные показатели качества регулирования, которые численно равны определённым интегралам во времени от некоторых функций отклонений регулируемой величины 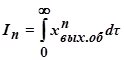, где n – показатель степени функции отклонений.

Интегралы такого вида численно равны площади, заключённой между функцией и осью времени (заштрихована на рис.3.10) и могут быть потому оценкой отклонений величины в процессе регулирования. Интегральный показатель качества при может быть применим только для апериодических процессов регулирования, так как при колебательных процессах площади, расположенные выше и ниже оси времени, взаимно уничтожаются и интеграл не отражает величины отклонений. Наиболее распространённым является квадратичный интегральный показатель , который характеризует отклонения при любом виде переходного процесса.

6.Показатели качества при позиционном регулировании, сопровождающемся автоколебательным характером изменения регулируемой величины. Ими являются амплитуда А_п и период Т_п колебаний. При несимметричном характере колебаний регулируемой величины относительно заданного значения х_здополнительным показателем качества регулирования служит отклонения среднего значения х от х_з.

Требуемое качество регулирования зависит от условий протекания технологического процесса и работы агрегата. В каждом конкретном случае выявляются наиболее существенные показатели качества регулирования, соблюдение которых обеспечивает рациональное функционирование производственного процесса. В некоторых случаях решающее значение имеет максимальное динамическое отклонение параметра, в других – интегральный показатель или время регулирования.

Рис.5.60.Типовые оптимальные процессы регулирования: а - апериодический с минимальным временем регулирования; б – процесс 20%-ным перерегулированием и минимальным временем первого полупериода; в – процесс с минимальной квадратичной площадью отклонения

Качество регулирования определяется видом переходного процесса. Можно рекомендовать три типа процесса регулирования, показанных на рис.3.20, один из которых, как правило, удовлетворяет конкретным требованиям регулирования промышленного объекта:

1)апериодический процесс с минимальным временем регулирования, рис.5.60, а;

2)процесс с 20%-ным перерегулированием и минимальным временем первого полупериода колебаний, рис.5.60, б;

3)процесс с минимальным квадратичным интегральным показателем, рис.5.60, в, 40-45% перерегулирование.

Переходные функция системы. При исследовании САУ (САР) в рассмотрение часто вводят некоторые типовые управляющие сигналы. К их числу относятся единичное ступенчатое воздействие, воздействие в виде дельта - функции, гармоническое воздействие, воздействие в виде полинома от [

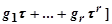и др.

При использовании единичного ступенчатого воздействия

вводится понятие переходной функции 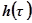, которая является одной из основных характеристик системы.

Переходной функцией САР называется переходной процесс системы, вызванный единичным ступенчатым воздействием при нулевых начальных условиях.

Используя понятие передаточной функции замкнутой системы, а также применяя обратное преобразование Лапласа, можно для переходного процесса написать

Если изображение управляющего сигнала является изображением единичного ступенчатого воздействия и равно 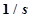, то предыдущее соотношение будет определять переходную функцию системы и может быть записано в виде .

Эта формула характеризует реакцию системы на единичный скачок и является переходной функцией. Изображение выходного сигнала представим в виде

Если учесть, что - переходная функция; - значение входного сигнала в момент , то применение теоремы свёртки в вещественной области даёт .

Это выражение называется интегралом Дюамеля и устанавливает связь между переходным процессом , вызванным любым воздействием, и переходной функцией .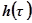

Интеграл Дюамеля имеет и другие формы записи:

Пусть некоторая функция имеет максимум при , является быстро убывающей при изменении в обе стороны от и определяет площадь, ограниченную кривой и осью абсцисс, равную единице. Функций, удовлетворяющих этим условиям, существует много. Одна из них =

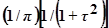и показана на рис.5.61, а.

Рис.5.61.Единичная импульсная функция или дельта-функция

Из свойств дельта - функции вытекает основные соотношения ; ,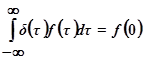

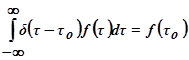Доказательство которых основано на том, что дельта – функция равна нулю везде, за исключением значения

, или .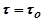

Последнее утверждение позволяет заменить бесконечно большие пределы интегрирования бесконечно малыми . Поэтому

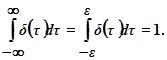
Рис.5.62.Дельта – функция и её спектральная характеристика

Понятие дельта – функции можно применить для записи других функций. Например, в случае единичного скачка имеем .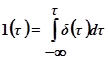

Спектральная характеристика дельта – функции может быть определена, если воспользоваться преобразованием Фурье

=. Модель спектральной характеристики дельта функции равен единице во всём диапазоне частот от - до +(рис.5.62).

Реакция системы на воздействие в виде дельта – функции при нулевых начальных условиях называется импульсной переходной функцией или весовой функцией. При этом процесс регулирования будет соответствовать интегралу , который определяет реакцию динамической системы на дельта – функцию, или импульсную переходную функцию. Между переходной и импульсной переходными функциями существует связь, выражающаяся равенством .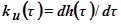

Пример. Управляющее воздействие, изменяющееся по закону , поступает на вход системы, передаточная функция которой в разомкнутом состоянии .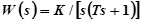

Требуется вычислить ошибку в установившемся режиме.

Передаточная функция ошибки для заданной системы

Делением полинома числителя на полином знаменателя этого уравнения получим ряд

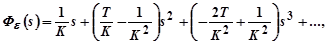
или после умножения на изображение входного сигнала

Сравнивая коэффициенты при одинаковых степенях в последнем выражении и в выражении , найдём коэффициенты ошибок для системы с астатизмом первого порядка: …

Определив производные управляющего воздействия (остальные производные равны нулю) и подставив их вместе с коэффициентами ошибок в уравнение 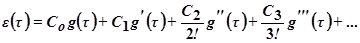, найдём установившуюся ошибку:

Если записать обратное преобразование Лапласа для выражения

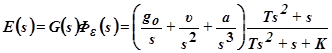
и не учитывать в оригинале составляющие, обусловленные полюсами передаточной функции ошибки, то получим результат, совпадающий с предыдущим уравнением.

Устойчивость САР (САУ) является важнейшим показателем качества процесса регулирования (управления). Общий критерий устойчивости динамических систем был сформулирован крупнейшим русским математиком и механиком А.М.Ляпуновым.

Пусть некоторая система находится в установившемся состоянии и затем была выведена из него какими – либо возмущениями, которые в момент (начало отсчёта времени) были сняты либо скомпенсированы. С этого момента начинается свободное движение системы. Отклонения от установившегося состояния, образовавшиеся к моменту (называемые начальными отклонениями), могут при свободном движении и безгранично нарастать либо стремиться к какой–нибудь конечной величине или нулю.

Система называется устойчивой (или асимптотически устойчивой) лишь в последнем случае, т.е. если при свободном движении начальные отклонения с течением времени стремятся к нулю и, следовательно, система возвращается к своему исходному, невозмущённому состоянию. Во всех остальных случаях система неустойчива.

Из неустойчивых систем иногда выделяю такие, у которых начальные отклонения при стремятся к постоянной конечной величине; эти системы называются нейтральными.

Устойчивость системы тесно связана с предельным значением её импульсной переходной характеристики , так как приложенный к входу системы импульс создаёт весьма кратковременное воздействие, выводящее систему из исходного установившегося состояния, после чего начинается её свободное движение. Следовательно, устойчивость, неустойчивость и нейтральность системы определяются соответственно тремя условиями: , и .

При действии возмущений устойчивые и неустойчивые системы ведут по – разному. Рассмотрим поведение САР, находившейся в установившемся (равновесном) состоянии неопределённое время. Внезапно в момент появилось единичное возмущение (например, изменилась нагрузка ТОУ), которое выведёт объект из равновесного состояния, и регулируемый параметр начнёт изменяться – появится его отклонение от установившегося состояния. Теперь начнёт срабатывать регулятор, устраняя влияние возмущения на регулируемый параметр ТОУ. Значение этого параметра с течением времени под влиянием деятельности будет изменяться.

При этом возможны пять основных случаев (при неограниченной длительности, т.е. при ; рис.5.63).

1.Регулируемый параметр принимает значение, имевшее место до появления возмущения (следовательно, регулятор астатический). При этом переходный процесс может быть не колебательным и колебательно – затухающим (кривые 1, 2 и 3). Подобные системы считаются устойчивыми (с астатическим регулированием).

2.Регулируемый параметр (т.е. регулятор статический). И тут переходный процесс может быть монотонным, не колебательным с затуханием (кривые 4 и 5). Подобные системы также считаются устойчивыми (со статическим регулированием).

3.Регулируемый параметр изменяется по периодическому закону, совершая незатухающие колебания с постоянной амплитудой вокруг среднего значения (кривые 6). Подобным характер изменения во времени регулируемого параметра может являться результатом двух обстоятельств.

Во – первых, линейная система может находиться на границе устойчивости: ничтожное изменение параметров системы в ту или иную сторону превращает её в устойчивою или, соответственно, неустойчивую, и колебания параметра становятся затухающими или расходящимися. Естественно, что подобные САР не имеют никаких резервов устойчивости, а поэтому не должны применяться, ибо небольшие ошибки (допуски, округления) при проектировании и изготовлении могут привести систему к потере устойчивости.

Во – вторых, у нелинейных систем могут возникать незатухающие колебания с постоянной амплитудой при отсутствии возмущений (например, при скачкообразном возмущении и последующем свободном движении). Эти колебания называются автоколебания. Возникновение автоколебаний обусловлено равенством потерь энергии (за период колебаний). Автоколебания не превышаются в расходящиеся при изменении начальных отклонений (в определённых границах). Несмотря на то что САР с автоколебаниями и не удовлетворяют общему критерию устойчивости, они тем не менее часто применяются (благодаря простое регулирующих устройств) в тех случаях, когда не требуется постоянства регулируемого параметра и допустимы его незатухающие колебания с некоторой амплитудой вокруг заданной величины.

4.Регулируемый параметр совершает колебания с неограниченно возрастающей амплитудой (кривая 7). Эти системы являются неустойчивыми (расходящимися).

5.Регулируемый параметр монотонно неограниченно возрастает с течением времени (кривая 8). Подобные системы также являются неустойчивыми (расходящимися).

Устойчивость САР может быть связана с двумя обстоятельствами.

Во – первых, система может быть построена так структурно, что вне зависимости от её параметров всегда является неустойчивой. Добиться устойчивости подобной системы можно лишь изменением её структуры. Подобные системы называются структурно – неустойчивыми.

Во – вторых, система может быть устойчивой или неустойчивой в зависимости от значений её параметров (т.е. от постоянных времени – Т и коэффициентов передачи – k). Иначе говоря, имеются границы совокупностей значений параметров системы, при которых она является устойчивой, а за пределами которых устойчивость теряется. Подобные системы называются структурно – устойчивыми.

При этом особенно важно, чтобы значения заданных и конструктивных параметров системы всегда находились в границах, обеспечивающих устойчивость систем при изменении настроечных параметров в определённых пределах. Благодаря этому особое значение приобретает проблема определение структурной устойчивости САР (САУ).

Нетрудно доказать, что указанные ранее два режима устойчивых САР при единичном возмущении имеют место лишь при соблюдении общего критерия устойчивости. Иначе говоря, нужно убедиться в том, что уравнение свободного движения

, (где - операторный полином замкнутой САР) удовлетворяется одновременно с неоднородным дифференциальным уравнением возмущённого движения: .

Развернув значение операторного полинома , в общем случае получим

Введём вместо новую переменную . Коэффициент - постоянная величина; следовательно, или , т.е. операторный полином здесь такой же, как и при свободном движении системы; следовательно, это дифференциальное уравнение удовлетворяется при лишь в том случае, когда при свободном движении .

Для решения уравнения свободного движения нужно найти корни характеристического уравнения: =0.

Левая часть характеристического уравнения может быть разложена на множители (число корней равно порядку уравнения): , где - корни характеристического уравнения.

Следовательно, решение уравнения свободного движения принимает общий вид (при переходе от показательных комплексных функций к тригонометрическим):

+ .

Первая сумма в правой части относится к вещественным корням и характеризует экспоненты с положительными, отрицательными и нулевыми показателями. При отрицательных показателях ординаты экспоненты стремятся к нулю, при нулевых – к постоянным величинам (), а при положительных – к бесконечности. Вторая сумма относится к комплексным корням и характеризует расходящиеся (при ) и затухающие (при ) колебания. Четвёртая сумма относится к кратным вещественным корням с кратностью . Все слагаемые этой суммы (относящиеся к кратным корням) при и отрицательных стремятся к нулю, а при положительных - к бесконечности.

Поскольку относительное отклонение представляет собой сумму рассмотренных членов, совершенно очевидно, что и САР является устойчивой лишь в том случае, когда все вещественные корни и действительные части комплексных корней характеристического уравнения системы отрицательны.

На комплексной плоскости (рис.5.64) действительные отрицательные корни располагаются на оси абсцисс (вещественной оси Re) слева от начала координат, сопряжённые мнимые корни – на оси ординат (мнимой оси Im), а сопряжённые комплексные корни с отрицательными вещественными частями – в обоих левых квадрантах; нулевые корни располагаются в начале координат.

Следовательно, необходимым и достаточным условием устойчивости системы является расположение всех корней характеристического уравнения слева от мнимой оси.

Во многих случаях от САР для её надёжной, устойчивой работы требуется, чтобы корни характеристического уравнения располагались в левой полуплоскости в области, ограниченной двумя лучами, выходящими из начала координат и образующими с отрицательной вещественной полуосью углы не выше заданного угла . Так как для корня () угол радиус – вектора относительно указанной вещественной полуоси равен , где - Колебательность, то указанное выше требования сводится к тому, что для всех корней сводится к тому, что для всех корней характеристического уравнения системы колебательность не должна превышать .

Весьма существенно, что устойчивость линейной системы определяется лишь знаками вещественных частей корней и не зависит от значений постоянных интегрирования в последнем уравнении, т.е. от начальных условий. Иначе говоря, устойчивость системы сохраняется (или, наоборот, отсутствует) при любых начальных условиях.

Понятие устойчивости системы имеет три разновидности: устойчивость «малом», устойчивость в «большом» и устойчивость в «целом». Система считается устойчивой в «малом», если при начальных отклонениях, находящихся в некоторых малых пределах, и последующем свободном движении системы восстанавливается исходный равновесный режим. Иначе говоря, в данном случае устанавливается наличие области начальных отклонений, по отношению к которым система устойчива, без определения границ этой области и сопоставления их с реальными условиями.

Устойчивость системы в «большом» имеет место тогда, когда известны границы области начальных отклонений, при которых свободное движение приводит к возврату системы к исходному равновесному режиму, причём установлено, что реальное (возможные) начальные отклонения находятся внутри указанных границ.

Система устойчива в «целом» или неограниченно устойчива (декремента) в том случае, когда область начальных отклонений, при которой восстанавливается исходное равновесное состояние системы вообще не ограничена.

Линейная система при устойчивости в «малом» устойчива как в «большом», так и в «целом».

Реальные САР содержат очень часто и нелинейные звенья. Обычно, если эти звенья линеаризуются (для рабочего диапазона), составляется линейная модель реальной системы и изучается указанными ранее методами устойчивость этой модели. Если модель построена путём перехода к малым отклонениям (т.е. методом, рассмотренным ранее, когда функция разлагается в ряд Тейлора с использованием первых двух членов), то устойчивость линейной модели подтверждает устойчивость в «малом» реальной системы. Если же линейная модель строится путём экспериментального усреднения нелинейности системы путём экспериментального усреднения нелинейности системы (например, по экспериментальным частотным или временным характеристикам), то устойчивость линейной модели не гарантирует даже устойчивости в «малом» реальной системы. Поэтому для таких САР окончательное суждение об устойчивости можно сделать лишь после соответствующего суждения об устойчивости можно сделать лишь после соответствующего эксперимента, опыта наладки и подтверждения ими результатов анализа линейной модели.

Для исследования устойчивости САР широкого использования алгебраические и частотные метода.

Решение характеристических уравнений четвёртого и выше довольно громоздко либо невозможно в общем виде. Необходимые и достаточные условия устойчивости системы любого порядка без решения характеристического уравнения, но с введением в рассмотрение его коэффициентов, были найдены и сформулированы Раусом – Гурвицом.

Корни характеристического уравнения отрицательны или имеют отрицательные вещественные части при двух условиях:

o все коэффициенты положительны;

o некоторые комбинаций этих коэффициентов должны иметь определённый знак.

Второе условие может быть, согласно критерия Гурвица, дано в форме условия положительности всех определителей, составленных из постоянных коэффициентов

; ; и т.д. до .

Очевидны, что для систем первого и второго порядка критерий Гурвица вырождается в одно условие: коэффициенты характеристического уравнения должны быть одного знака.

Пример. Проверить устойчивость САР с операторным полиномом

Решение. Характеристическое уравнение имеет вид его коэффициенты , т.е. все они положительны. Следовательно первое условие устойчивости системы соблюдается.

Составим определители Гурвица; их будет три, так как характеристическое уравнение – третьей степени:

Второе условие критерия Гурвица также соблюдается; следовательно, система является устойчивой.

Частотные критерии устойчивости динамических систем базируются на принципе аргумента.

По аналогии с из любого полинома при замене получим комплексное число

Каждый из комплексных сомножителей представляет собой вектор в точке и концом на мнимой оси плоскости корней в точке (рис.3.25, а). При изменении ω от - до такой вектор опишет угол , если корень расположен в левой полуплоскости, и угол - , если находится в правой полуплоскости (рис.3.25, б). Модули этих векторов всегда больше нуля.

Для вектора приращение аргумента при изменении ω от - до будет, очевидно, равно алгебраической сумме приращений аргументов всех сомножителей:

где m – число корней, расположенных в правой полуплоскости.

Иначе говоря, получаем следующую формулировку принципа аргумента: приращение аргумента комплексного полинома при изменении ω от - до равно , умноженному на разность чисел корней, расположенных в левой и правой полуплоскостях.

Нетрудно видеть, что наличие корней, расположенных на мнимой оси (т.е. мнимых, например, для консервативного звена), приводит к скачкообразному изменению аргумента вектора для каждого корня на в зависимости от стороны подхода к оси ) при частоте ω_i, равной мнимой части корня. Естественно, что нулевой корень (например, для интегрирующего звена) также приводит к скачку аргумента на при .

Из сказанного следует, что при построении годографа вектора (порядок n которого известен) для изменения ω от - до можно судить о знаках корней уравнения . Так, например, при плавном протекании годографа справа от мнимой оси располагаются корней: , а слева от мнимой оси – остальные корней: . При .

Критерий устойчивости Михайлова базируется на рассмотренном выше принципе аргумента с использованием выведенного условия: динамическая система устойчива, если все n корней её характеристического уравнения расположены в левой полуплоскости.

Годограф характеристического вектора замкнутой системы при изменении ω от - до

называемый годографом Михайлова, имеет вещественную часть, чётную относительно ω, и мнимую часть, нечётную относительно ω. Поэтому ветвь годографа Михайлова при симметричная (относительно оси Re) ветви при . Отсюда, пользуясь принципом аргумента для , получаем критерий Михайлова: при изменении ωот0 до характеристической вектор замкнутой устойчивой системы никогда не равен нулю и монотонно поворачивается против часовой стрелки (т.е. в положительном направлении) от положительного направления вещественной оси на угол , где - степень характеристического уравнения.

Если годограф характеристического вектора удовлетворяет требованиям критерия Михайлова, то такой годограф и его протекание называется правильными, в противном случае – неправильными.

Рис.5.66.Кривые Михайлова для устойчивых систем.

Рис.5.67.Кривые Михайлова для не устойчивых систем (а) и (б-кривая 1); (б) устойчивой системы (б – кривая 2)

На рис.5.66 показаны кривые Михайлова для устойчивых систем, порядок характеристических уравнений которых n=1, 3, 5. При n=3 вектор , поворачиваясь вокруг начала координат против часовой стрелки при возрастании частоты, последовательно проходит три квадранта: I, IIиIII.В Ш квадранте модуль вектора становится бесконечно большим. При n= 5 вектор проходит I, II, III, IV и снова Iквадранты. При этом вектор нигде не обращается в ноль.

Если условия, сформулированные в критерии, нарушаются, то система становится неустойчивой (рис.5.67). Признаками неустойчивости могут служить следующие случаи: кривая Михайлова начинается не на положительно действительной оси (годограф 1 для n= 1 на рис.5.67, а); нарушается порядок прохождения квадрантов характеристическим вектором (например, годограф 2 для n= 2 на рис.5.67, а). Если кривая Михайлова проходит через начало координат (например, годограф 1 для n= 3 на рис.5.67, б), то это свидетельствует о наличии в характеристическом уравнении сопряжённых мнимых корней.

Пример. Проверить устойчивость САР, описываемой уравнением (для свободного движения)

Решение. В операторной форме характеристическое уравнение системы . Заменив , получим вектор Михайлова: , где ;

. Аргумент вектора Михайлова

; его модуль .

Найдём несколько характерных значений модуля (рис.5.68).

Пересечение годографа с действительной осью соответствует условию равенства нулю мнимой части вектора (для ): , откуда . При этом .

Эти два значения модуля отвечают двум пересечениям годографа с действительной осью (при аргументе 0 и π).

Пересечение годографа с мнимой осью отвечает условию : , откуда .

С мнимой осью годографа в одной точке (при аргументе π/2). С увеличением модуль характеристического вектора возрастает и ; никогда этот модуль не будет равен нулю, а угол поворота этого вектора против часовой стрелки будет монотонно стремиться к 3π/2. Следовательно, проверка по критерию Михайлова убеждает в устойчивости рассматриваемой САР.

Проверим правило чередования корней. Для мнимой части имеем два корня: 0 и 2,55; для вещественной части – один корень: 0,82. Таким образом корни чередуются.

Пример. Передаточная функция разомкнутой системы по управляющему воздействию определяется неустойчивым апериодическим звеном Применяя критерий Михайлова, оценить устойчивость замкнутой системы.

Находим передаточную функцию замкнутой системы:

По знаменателю этого выражения определяем уравнение характеристической кривой

где .

Действительная и мнимая части вектора позволяют построить годограф, который показан на рис.3.27, а в виде прямой I для К<1. Так как кривая Михайлова при = 0 начинается не на положительной действительной оси, то условия критерия не выполняются и система в замкнутом состоянии будет неустойчивой.

Если к>1, то годограф переместится I квадрант, что будет соответствовать выполнению условий критерия Михайлова и устойчивости системы в замкнутом состоянии.

Пример. Передаточная функция разомкнутой системы имеет вид и соответствует последовательному соединению интегрирующего и неустойчивого апериодического звеньев.

Оценить устойчивость системы в замкнутом состоянии. Передаточная функция замкнутой системы позволяет найти уравнение годографа

, где ; .

Действительная и мнимая части последних уравнений показывают, что кривая Михайлова начинается на положительном направлении действительной оси (кривая 2, рис.3.27, а), но проходит сначала IV, а затем III квадранты, что не соответствует условиям критерия. Следовательно, система в замкнутом состоянии неустойчива.

Пример. Передаточная функция замкнутой системы .

Характеристическое уравнение и уравнение кривой Михайлова имею третий порядок, т.е. n=3. Действительная и мнимая части вектора равны соответственно: ;

Кривая Михайлова, построенная по последним уравнением, может занимать различные положения на комплексной плоскости, определяемые соотношением параметров .

Так, например, если , то годограф будет соответствовать кривой 2 (рис.5.67, а), что отвечает выполнению условий критерия. Следовательно, система устойчива.

При годограф 1 (рис.5.67, б) проходит через начало координат при частоте . Система находится на границе устойчивости. В этом случае характеристическое уравнение имеет два сопряжённых мнимых корня, в чём легко убедиться, осуществляя подстановку в это уравнение. После подстановки характеристическое уравнение принимает вид . Поочерёдным приравниванием нулю сомножителей легко найти корни уравнения. В частности, уравнение даёт два сопряжённых мнимых корня: что указывает на существование в системе незатухающих колебаний с частотой .

Рис.5.69.Графики функцийи

При построении кривой Михайлова вектор разбивается на вещественную и мнимая части, которые являются функциями частоты. Построив графики этих функций, можно по расположению корней уравнений и на оси частот судить об устойчивости системы, приведённой на рис.3.29, где - корни уравнения ; - корни уравнения . Так как для устойчивости системы вектор в соответствии с критерием Михайлова последовательно проходит квадрантов, то, очевидно, при этом поочерёдно будут обращаться в ноль то вещественная, то мнимая части .

Следовательно между двумя соседними нулями функции должен находиться нуль функции . Иначе говоря, корни уравнений и должны обладать свойством перемежаемости. В случае нарушения этого свойства система неустойчива. На рис.5.69, а приводятся графики устойчивой системы, а на рис.5.69, б – графики неустойчивой системы.

Годограф характеристического вектора системы в любом случае можно построить непосредственно на основе характеристического уравнения системы, Для одноконтурных САР со статическими звеньями и без дифференцирующих звеньев годограф характеристического вектора может быть построен и по годографам отдельных звеньев, образующих систему.

В этом случае входные операторы всех звеньев вырождаются в коэффициенты усиления и формируют общий коэффициент усиления разомкнутой системы. Тогда операторный полином системы принимает следующий вид:

где . - вещественная постоянная величина.

Соответствующее характеристическое уравнение имеет вид .

Заменим в характеристическом уравнении или

Кроме того, для каждого звена может написать выражение его характеристического вектора .

Очевидно, что получим перемножением векторов звеньев (умножением их модулей и сложением их аргументов) .

Следовательно, характеристический вектор системы отличается от произведения векторов отдельных звеньев, образующих эту систему, на постоянную величину (рис.5.70, а). Чтобы найти его, нужно переместить конец вектора 1, равного произведению векторов отдельных звеньев, вправо на величину - вектор 2 (с сохранением ординаты) или же сдвинуть влево начало этого вектора (т.е. начало координат) на туже величину - вектор 3.

Очевидно, что годограф характеристического вектора САР можно получить из годографов отдельных звеньев аналогично, т.е. перемножением соответствующих векторов (эти операции называются перемножением годографов звеньев), а затем смещением вправо полученной кривой или перемещением влево начало координат (т.е. мнимой оси) на величину коэффициента усиления (рис.5.70, б).

Построим годографы типовых звеньев (рис.3.32). Для статического звена:

Следовательно, при изменении конец вектора будет скользить вверх вдоль вертикали, расположенной вправо от начала координат на расстоянии «+1»(рис.5.71, а). Годограф представляет собой эту вертикаль, не выходящую за пределы первой четверти, т.е. годограф правильный (характеристическое уравнение звена первой ступени).

т.е. годограф неправильный – это вертикаль во второй четверти, сдвинутая влево от начала координат на величину «-1»(рис.5.71, б).

Для интегрирующего звена:

т.е. годограф совмещается с мнимой полуосью ; годограф неправильный (рис.5.71, в).

Для колебательного звена:

;

С изменением значение Im растёт монотонно от , а меняется монотонно от 1 (), проходит через 0 (при , здесь ) и неограниченно возрастает по абсолютной величине, достигая (рис.5.71, г); годограф правильный – при второй степени характеристического уравнения размещается в первых двух четвертях.

т.е. все точки годографа лежат на оси ; следовательно годограф неправильный (рис.5.71, д). При значение =1, при -Re=0, при дальнейшем неограниченном увеличении величина также неограниченно возрастает по абсолютной величине.

Для идеального дифференцирующего звена и, следовательно,

т.е. годограф вырождается в точку, расположенную на действительной оси на расстоянии «+1» от начала координат.

Для инерционно – форсирующего звена:

т.е. характеристический полином и, очевидно, годограф характеристического вектора будут, такими же, как у статического звена, рассмотренного выше.

Критерий Михайлова позволяет оценивать устойчивость системы при непосредственном использовании характеристического уравнения замкнутой системы. Вместе с тем, руководствуясь основными положениями критерия Михайлова, можно составить суждение об устойчивости замкнутой системы по АФХ разомкнутой системы.

Пусть имеется передаточная функция разомкнутой системы, которая при замене на превращается в выражение АФХ , в котором порядок полинома числителя для реально существующих систем не превышает порядка полинома знаменателя. В крайнем случае порядки полиномов равны. Знаменатель последнего выражения определяет характеристическое уравнение разомкнутой системы.

Рис.5.72.Годографы Михайлова

Допустим, что разомкнутая система устойчива и все корни характеристического уравнения находятся в левой полуплоскости. Нулевых и мнимых корней нет. Применяя критерий Михайлова, построим характеристическую кривую на комплексной плоскости. Полагаем, что этот годограф имеет вид кривой (рис.5.72, а), соответствующей устойчивой разомкнутой системе.

Для замкнутой системы

где .

Характеристическое уравнение замкнутой системы определяется знаменателем передаточной функции или выражением .

Система, устойчивая в разомкнутом состоянии, может оказаться неустойчивой в замкнутом состоянии. Сделаем предположение, что замкнутая система находится на границе устойчивости и что кривая Михайлова (рис.5.72, а)

проходит через начало координат при частоте