Контакт цилиндров из однородных материалов
Схема контакта двух цилиндров
Контактные напряжения
Контактными называют напряжения в зоне контакта деталей машин. На практике часто появляется необходимость определения напряжений и деформаций в этих зонах как при расчете на контактную прочность (зубчатые и фрикционные передачи), так и для оценки предела выносливости (резьбовые и прессовые соединения и др.).
Конструкционные контактные задачи решают методами теории упругости, как правило, приближенно. Достаточно точные решения получены лишь для задач об упругом контакте деталей простой формы (цилиндры, шары и т. п.).
Для понимания принципиального подхода при решении контактных задач рассмотрим взаимодействие цилиндров (задача Герца).
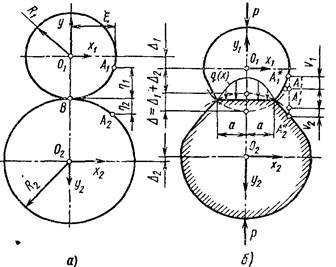
Рассмотрим напряженное состояние двух длинных цилиндров с параллельными осями (а), сжатых распределенными по длине радиальными нагрузками р (б). На расстоянии x от плоскости, проходящей через оси цилиндров, возьмем две точки A1 и А2,. Если контакт цилиндров без нагрузки происходил по линии, параллельной их осям через точку В, то расстояние между этими точками вдоль оси у равно (см. рис.а)
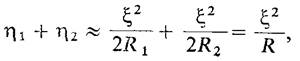
Условие совместности перемещений*
R1 и R2. — радиусы первого и второго цилиндров; R — «средним» радиус кривизны 1/R = 0,5(1/R+ 1/R) ;
Под действием распределенной нагрузки р произойдет деформация цилиндров в зоне контакта, а их оси переместятся к этой зоне на величины D1, и D2. Общее сближение осей (см. рис. б) D = D1 + D2. Точки займут новое поверхности цилиндров, получив перемещения положение А¢1 и А¢2. , а точки, равные v1 и v2, займут положения A*1 и А*2. В зоне контакта точки А*1 и А*2 совместятся и потому

Это равенство выражает условие совместности перемещений контактирующих точек цилиндров и показывает, что перемещения осей цилиндров под нагрузкой вызывают смещения точек в результате деформации.
Распределение давлений по площадке*
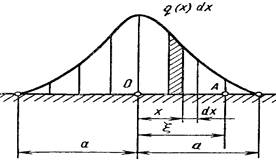
Если трение отсутствует, то в точках контакта будут действовать лишь нормальные давления q (x), и условие равновесия примет вид
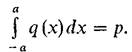
Выражая смещения v через контактные давления q, используя модуль упругости Е и коэффициент Пуассона n по теории упругости (задача Фламана), имеем закон распределения давлений по ширине
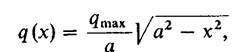 где а –половина ширины контакта
где а –половина ширины контакта
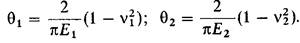
Тогда имеем:
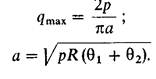
Если цилиндры изготовлены из материалов, у которых Е1 = E2 и n1 = n2 = 0,3, то
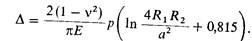
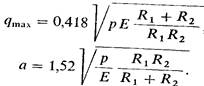
Так как полуширина контактной площадки а зависит от р, то смещение D является нелинейной функцией от р, хотя материал цилиндров предполагается упругим. Это объясняется изменением а в процессе нагружения: значение а возрастает по мере увеличения р, и относительная податливость контактной зоны уменьшается.
Эта задача, впервые решенная Г. Герцем, широко применяется в расчетах на контактную прочность деталей 'машин конечной длины(фрикционных и зубчатых передач и др.)..