Лекция 7. Расчёт ступени центробежного насоса.
Определение частоты вращения ротора насоса n. При известных значениях расхода жидкости Q и удельной работы ступени L частота вращения ротора n определяется с учётом существующих ограничений на этот параметр. Эти ограничения связаны со значением коэффициента быстроходности ns и кавитационными качествами проектируемого насоса. На стадии проектирования кавитационные качества могут быть определены на основе учёта значений группы так называемых установочных параметров и кавитационного коэффициента быстроходности C.
Учёт названных ограничений обеспечивается, если принимаемая частота вращения ротора удовлетворяет трём выражениям:
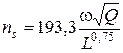 (7.1)
(7.1)
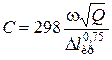 (7.2)
(7.2)
 (7.3)
(7.3)
Для того, чтобы проектируемый насос соответствовал желательному типу гидравлических машин, следует выбрать определённый диапазон ns, внутри которого такой тип может обеспечить наивысший КПД (см. лекцию 5, рис.5.1). Например, чтобы спроектировать под заданные Q и L наиболее простой центробежный насос с цилиндрическими лопастями одинарной кривизны, следует выбрать ns = 40…80.
Кавитационные качества насоса, как это объяснялось в предыдущей лекции, определяются, с одной стороны, значением коэффициента C в (7.2), а с другой стороны, параметрами величин, входящих в (7.3). Так, для насосов внутреннего контура систем охлаждения ДВС рекомендуется C = 1100…1400, для насосов контура забортной воды C = 900…1100.
В (7.3) значения параметров правой части принимаются в зависимости от условий применения насоса.
Так, для определения удельных потерь на всасывании lтр.п необходимо располагать как минимум схемой рассматривай системы охлаждения, из которой можно установить диаметр трубопровода, его длину и наличие тех или иных характерных сопротивлений на этом участке (фильтров, задвижек, поворотов потока, т.п.). При этих данных величина lтр.п рассчитывается на основании рассмотренных выше зависимостей.
Допустимая величина высоты всасывания Hвс.д также назначается с учётом места расположения насоса в проектируемой системе охлаждения и с учётом его возможного положения относительно уровня воды в приёмном водоёме (баке). Если насос может находиться над уровнем жидкости, то Hвс.д > 0. В ином случае можно принимать Hвс.д < 0.
Давление над уровнем жидкости в приёмном баке pa может быть атмосферным или отличным от него, также в зависимости от схемы и особенностей системы охлаждения.
Давление парциальных паров воды pп выбирается по термодинамическим таблицам, определяющих состояние воды на линии насыщения в функции от температуры воды.
Плотность воды обычно принимается 1000 кг/м3, но в точных расчётах может корректироваться в зависимости от наличия специальных присадок или от солёности.
Коэффициент запаса А определяется в зависимости от назначения и ряда особенностей насоса по формулам ГОСТа. При этом учитывается величина Δlкр, отношение D2/D0, а также состав воды. Коэффициент запаса А может изменяться примерно от 1,05 до 1,35.
Поскольку многие из входящих в систему (6.1) – (6.3) параметров выбираются независимо друг от друга, то не исключена ситуация, когда невозможно определить такую частоту вращения ротора (или однозначно связанную с ней угловую скорость вращения ротора), которая будет удовлетворять этой системе. В таком случае следует изменить в исходных данных те параметры, которые позволительно изменять по условиям проектирования. Обычно в этом случае вначале изменяют ns в пределах возможных диапазонов его изменения, а если этого недостаточно, то корректируют те параметры выражения (7.3), которые допустимо изменять с учётом принятых ограничений.
В общем случае ход определения искомого значения ω такой. Вначале вычисляется Δlкр по (7.3), затем находится ω на основании (7.2):
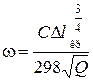 (7.4)
(7.4)
Далее по (7.1) определяется значение ns, соответствующее найденному значению ω. Если ns входит в выбранный диапазон значений, ω следует округлить до возможных скоростей вращения ротора, которые можно обеспечить выбранным приводным двигателем. По округлённому значению ω следует уточнить величину Δlкр, которая может быть обеспечена насосом с заданным С на основании (7.2):
 . (7.5)
. (7.5)
После этого проверяется высота всасывания, которая может обеспечиваться проектируемым насосом на основании (7.3):
 . (7.6)
. (7.6)
При Hвс >= Hвс.д расчёт закончен, в ином случае следует уменьшить ω, если это допускается условиями проектирования и повторить расчёты по (7.1),(7.5) и (7.6). Если подобные корректировки ω выводят ns из выбранного диапазона его значений, следует либо изменить этот диапазон, либо пересмотреть исходные данные, если это возможно, чтобы выполнить проектирование насоса в выбранном диапазоне ns.
Схема расчётов проточной части насоса. Расчёт проточной части насоса выполняется для определения всех геометрических размеров колеса и каналов корпуса. Расчёт начинается при заданных значениях Q, L, ω.
В начале расчёта определяются все диаметры рабочего колеса, начиная с диаметра вала do. Диаметр вала определяется в зависимости от крутящего момента на валу и прочности материала вала. Крутящий момент определяется в функции мощности привода и частоты вращения ротора. Мощность привода определяется через полезную мощность насоса и его КПД. КПД насоса η определяется как произведение объемного, гидравлического и механического КПД. Механический КПД вычисляется как произведение ηмвн, учитывающего потери на трение дисков колеса о воду, и ηсп, учитывающего потери в сальниках и подшипниках:
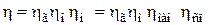 (7.8)
(7.8)
Для определения всех входящих в выражение (7.8) составляющих рекомендуются формулы
 ; (7.9)
; (7.9)
 . (7.10)
. (7.10)
Приведенный диаметр входа в колесо в первом приближении
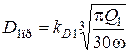 .
.
где Q1= Q/z расход жидкости через одно колесо; z- число параллельно включенных колес.
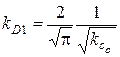 ;
;
 , (см. рис. 7.1)
, (см. рис. 7.1)

Рис.7.1
 ; (7.11)
; (7.11)
 . (7.12)
. (7.12)
Чтобы определить диаметр вала ротора насоса dв (рис.4.3), используется условие сохранения прочности вала при скручивании. На этом основании
 ,
,
где момент на валу:
 Нм,
Нм,
мощность на валу насоса:
 Вт.
Вт.
[τ] – допустимое напряжение на скручивание.
Рекомендуется принимать[τ] ≤ 300·105Па, что является заниженным значением; [τ] целесообразно занижать, чтобы косвенно учесть неизбежное влияние дополнительных нагрузок.
Диаметр ступицы рабочего колеса принимается конструктивно:

Ширина ступицы Вк определяется конструктивно:
 .
.

Рис.7.2
Диаметр входа в рабочее колесо определим на основе уравнения расхода
 ;
;
где . Qp - расход жидкости через колесо насоса
 ;
;
со - скорость жидкости в кольцевом приемном отверстии; определяется с учетом заданных кавитационных качеств насоса:
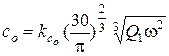 . (7.13)
. (7.13)
Диаметр входа в рабочее колесо
 .
.
Диаметр середины входной кромки лопасти для насосов с ns = 50... 120 находим по соотношению

В радиальных колесах (ns ≤ 70) входная кромка может располагаться за зоной поворота потока:
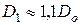
Сама кромка выполняется горизонтально или наклонно под углом до
30° к оси вращения (см. рис.7.2).
Окружная скорость на диаметре D2
 .
.
Считается, что после поворота потока в колесе вектор скорости направлен чисто радиально. Влиянием закрутки потока из-за трения о колесо пренебрегаем. Рекомендуется сохранять постоянными проходные сечения канала колеса от входа в колесо до входа на лопатки. Тогда скорость потока перед входом на лопатки

Поскольку эта скорость направлена по радиусу, то

где индекс «m» отмечает скорости и их составляющие, направленные по радиусу; штрих «'» отмечает скорости жидкости вне каналов колеса в незагроможденном потоке.
После поступления в межлопаточный канал поток увеличивает скорость из-за загромождения лопатками. Если fo – площадь сечения канала, перпендикулярного радиусу, без загромождения лопатками, a f1 - аналогичная площадь с учетом загромождения, то коэффициент загромождения на входе
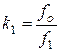 .
.
Обычно k1 = 1,1...1,25. Такое значение k1 следует принять ориентировочно в начале расчета. После завершения тех разделов расчета, где будут определены основные размеры колеса, эту величину следует уточнить по формуле, полученной на основании выражения ( ), и при необходимости вернуться к рассматриваемой стадии расчетов:

 .
.
где Δ1 - толщина лопасти на входе (см. рис.7.2). Обычно Δ1 = 1…4мм, выбирается из условия обеспечения прочности, но так, чтобы обеспечить k1 =1,1...1,25; β1 - угол установки лопасти на входе (см.рис.7.2); z - число лопастей.
Приняв k1 , найдем скорость с1m после поступления потока в межлопаточный канал:
 .
.
Располагая скоростями  , с1m и u1, строим треугольники скоростей на входе в точках до и после входа в межлопаточный канал, совместив их на одном чертеже (рис.7.2). Угол β1 должен быть в пределах 15…30о. При малых углах β1 возрастает длина лопасти и увеличиваются гидравлические потери.
, с1m и u1, строим треугольники скоростей на входе в точках до и после входа в межлопаточный канал, совместив их на одном чертеже (рис.7.2). Угол β1 должен быть в пределах 15…30о. При малых углах β1 возрастает длина лопасти и увеличиваются гидравлические потери.
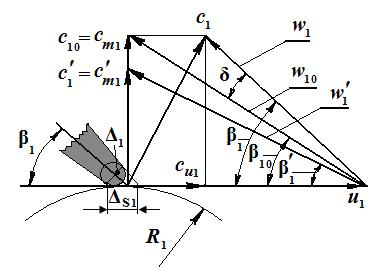
Рис. 7.3 Совмещённые треугольники скоростей на входе в колесо насоса
Угол безударного входа на лопатку.
 .
.
Для насосов охлаждения дизелей работа на расходах, выше расчетных, маловероятна. Поэтому введение больших углов атаки нецелесообразно. Впрочем, считается, что принятие δ до 15° не сказывается на величине потерь в насосе. Для обычного случая рекомендуем δ = 0…5о. Тогда угол установки лопасти на входе

В соответствии с построением на рис.7.3 относительные скорости входа потока на лопатку
 . (7.13)
. (7.13)
Наружный диаметр колеса зависит от формы лопастей, которая определяется углом β2. Выбранная форма лопастей при тех же условиях влияет на соотношение относительных скоростей потока в рабочем колесе. Установлено, что соотношение w1/ w2 оказывает определяющее влияние на величину гидравлических потерь в колесе и, соответственно, на величину гидравлического КПД. Для того, чтобы этот КПД, вычисленный ранее в функции от ns и соответствующий оптимальному для данного насоса значению, был получен при испытаниях проектируемого насоса, необходимо обеспечить рекомендуемое соотношение w1/ w2. Рекомендуемые значения w1/ w2 в функции от ns представлены на рис.7.4. Там же дана и полиномиальная форма соответствующей зависимости.
Для того, чтобы обеспечить желательное отношение w1/ w2, необходимо подобрать соответствующий угол установки лопасти на выходе β2 и значение меридианной составляющей абсолютной скорости на выходе c2m.
Особенностью рассматриваемой методики расчёта в данном случае является то, что соотношение w1/ w2 нельзя выразить в виде простой зависимости от β2 и c2m. Желательное соотношение w1/ w2 приходится обеспечивать путём ряда последовательных изменений β2 и c2m. Порядок вычислений по установлению оптимального соотношения w1/ w2 и по выбору соответствующего ему угла β2 следующий.
Выбрать значение c2m из соотношения
 . (7.14)
. (7.14)
Предварительно выбрать угол β2, следуя таким рекомендациям:
| ns | |||
| β2, град | 30…36 | 25…30 | 20…22 |
Определить число лопастей z в первом приближении по формуле Пфляйдерера

 , (7.14)
, (7.14)
где k = 6,5 для литых рабочих колёс, с относительно большой толщиной лопасти и k ≥ 8 для рабочих колёс с лопастями из листового материала.
Наружный диаметр колеса в этой формуле следует принять приближённо, в первом приближении, руководствуясь эмпирической зависимостью
 . (7.15)
. (7.15)
Полученное значение z округлить до целого. Для получения стабильной характеристики насоса должно соблюдаться условие: 10 ≥ z ≥ 6…7.
Далее найти поправку на конечное число лопастей:
 , (7.16)
, (7.16)
где
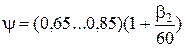
Далее определить удельную работу колеса с бесконечным числом лопастей
 ,
,
где Lт – теоретическая удельная работа
 .
.
Далее определяется диаметр D2 на основании уравнения Эйлера. При отсутствии закрутки потока на входе
 . (7.17)
. (7.17)
Размер D2, полученный из (7.16), сравнить с  , найденным из (7.15). При расхождении более принятой меры точности (обычно 3%) принять D2, полученный по (7.17) в качестве исходного, и повторять расчеты, начиная с (7.14) до (7.17), пока не будет обеспечена необходимая точность.
, найденным из (7.15). При расхождении более принятой меры точности (обычно 3%) принять D2, полученный по (7.17) в качестве исходного, и повторять расчеты, начиная с (7.14) до (7.17), пока не будет обеспечена необходимая точность.
После определения уточненного D2 следует найти w2. Он находится из треугольника скоростей на выходе из колеса (см. рис.7.3).
Для этого вначале находим
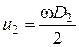 .
.
При известной скорости c2m находим
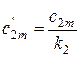 ,
,
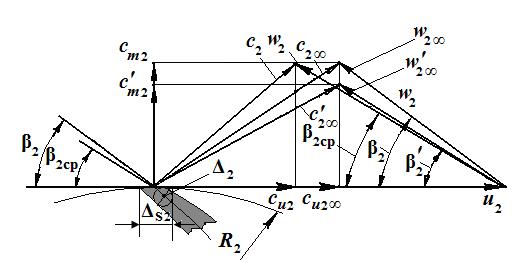
Рис.7.3 Треугольники скоростей на выходе из колеса
где k2 – коэффициент загромождения канала колеса лопатками на выходе
 .
.
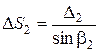 ,
,
где Δ2 – толщина лопасти на выходе; обычно Δ2 = 2...4 мм.
значения c2u и c2u∞ определяются следующим образом:
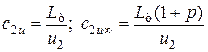 .
.
После определения переносной скорости u2 и проекций абсолютной скорости c2m,  , c2u , c2u∞ могут быть построены треугольники скоростей на выходе из колеса для z = ∞ и z ≠ ∞ (см. рис. 7.3). Способ построения треугольников понятен из рисунка.
, c2u , c2u∞ могут быть построены треугольники скоростей на выходе из колеса для z = ∞ и z ≠ ∞ (см. рис. 7.3). Способ построения треугольников понятен из рисунка.
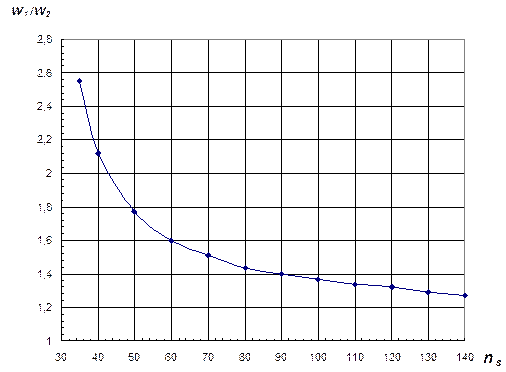
w1/ w2 = 3,166E-11 ns 6 - 1,812E-08 ns 6 + 4,228E-06 ns 4 - 5,150E-04 ns 3 + 3,464E-02 ns 2 - 1,231E+00 ns + 1,982E+01
Рис. 7.4 Значения оптимального соотношения w1/ w2 в зависимости от ns
В соответствии с рис.7.3 можно найти

и вычислить w1/ w2, где w1определено по (7.13).Если полученное отношение меньше оптимального, необходимо увеличить β2 и вновь повторить весь цикл расчетов с (7.14) no (7.18).
После определения D2 и оптимального значения β2 имеем окончательные значения w2 и u2. Для дальнейших расчетов необходимо также вычислить
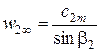 .
.
Конец