Ортогональное проецирование
Аксинометрическая плоскость
Аксонометрической называется проекция, у которой проекторы перпендикулярны плоскости проекции иначе имеем косоугольную проекцию.
Среди аксонометрических проекций различают:
1) Ортогональную проекцию – когда проекционная плоскость перпендикулярна главным координатным осям.
2) Изометрию , когда в плоскости проекции 3 оси одинакого сокращены.
3) Диметрию, когда в плоскости проекции 2 оси одинакого сокращены.
4) Триметрия – разное сокращение по всем 3 осям.
Рассмотрим часто употребляемое в техническом черчении ортогональное проецирование, которое слагается из фронтальных, профильных и горизонтальных проекций.
Рассмотрим проекции в плоскостях:
X=0, y=0 и z = 0
Преобразование проецирования на соответсвующую нклевую плоскость всегда содержит нулевой столбец соответствующий плоскости проекции, поэтому матрицы преобразования проецирования будут иметь следующий вид:
Матрицы преобразования проецирования в плоскостях X=0, Y=0, Z=0
M(X=0)= ,
,  ,
, 
Естественная видовая плоскость экрана xoy поэтом рассмотрим различные виды ортогональных проекций на плоскость z=0(имея ввиду, что на плоскости x=0 и y=0 всё выполняется аналогично).
Для того чтобы получить необходимый вид проекции необходимо:
1. Выполнить вращение объекта вокруг оси x или y, до тех пор, пока требуемый вид объекта не примет фронтальный вид.
2. Выполнить проецирование из бесконечности на плоскость z=0.
Тогда алгоритмы ортогонального проецирования запишутся как:
· M(Фп) = М(R(X,0)) * M(z=0)
фронтальная проекция, вид спереди.
· M(Фз) = M(R(X,180)) * M(z=0)
фронтальная проекция, вид с тыла.
· M(ФВ) = М(R(X,90)) * M(z=0)
горизонтальная проекция, вид сверху.
· M(ФН) = М(R(X,-90)) * M(z=0)
горизонтальная проекция, вид снизу.
· M(Фл) = М(R(Y,90)) * M(z=0)
профильная проекция, вид слева.
· M(Фп) = М(R(Y,-90)) * M(z=0)
профильная проекция, вид справа.
Подстовляя М(R(X,угол )) и M(R(Y,угол)), значение углов соответсвующих видовых преобразований, получим:
M(Фп)=
M(Фз)
M(Гв)=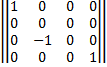
M(Гн)=
Профильные:
M(Гл)=
M(Фп)=
Эти матрицы составляют программное обеспечение ортогонального проецирования и после выполнения умножения матрицы описания объекта в ОК на соответсвующую матрицу видового преобразования, получаем нужную проекцию.
P*=P*M(вида)
Пример решения задач:
1. Рассмотрим примеры вычисления ортоганальных проекций для равнобедренной усечённой пирамиды (рис1 из лекции 1).

Запишем матрицу усечённой пирамиды в координатах
Построим профильную проекцию, вид слева
P*=P* =
=

Y*
3 b(c) a(d)
f(g) 1 2 e(i) X*
горизонтальная, вид сверху
 P*=P*
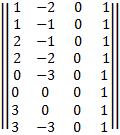
P*=P*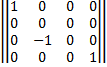 =
=
f 1 2 g 3 X*
-1 b c
-2 a d
-3
e i
Y