Электрическое поле системы двух точечных зарядов
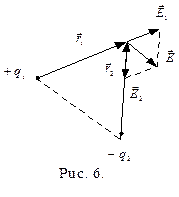Пример 3.1. В двух вершинах равностороннего треугольника со стороной 
расположены точечные заряды 
и 
.
Найти модуль напряженности электрического поля в третьей вершине треугольника?
Решение: Каждый заряд в третьей вершине треугольника создает поле напряженностью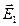 
и 
, векторы которых показаны на рис. 6. По принципу суперпозиции полей напряженность результирующего поля 
. Модуль вектора 
можно определить, используя теорему косинусов для треугольника, состоящего из векторов 
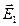,и
. Поскольку 
, а 
, 
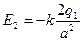, то
Ответ: 
Пример 3.2. Электростатическое поле на оси диполя.
Электрическим диполем называется система двух одинаковых по величине разноименных точечных зарядов 
и 
, расположенных на расстоянии 
друг от друга, которое значительно меньше расстояния от середины диполя до точки, в которой вычисляется поле системы. Прямая линия, проходящая через оба заряда, называется осью диполя.
Вычислить электрическое поле в точке М, лежащий на оси диполя, на расстоянии r от его середины (Рис.7).
Решение: Поле в точке М – это поле двух точечных зарядов, следовательно, 
. Направлен вектор по оси диполя и модуль его равен 
, где 
, 
- расстояние от середины диполя до точки поля. Тогда, учитывая, что 
, получим . 
(3.5)
Ответ: 
.
Пример 3.3. Вычислить электрическое поле в точке 
, лежащей на перпендикуляре к оси диполя и проходящем через его середину.
Решение: Напряженность поля в точке М равна векторной сумме напряженностей электрических полей двух точечных зарядов (Рис.8).
Модуль вектора напряженности электрического поля диполя можно определить из подобия треугольников
,
то есть 
или 
.
Учитывая, что 
, получим 
. (3.6)
Сравнивая результаты, полученные в примерах (3.2) и (3.3), уравнения (3.5) и (3.6) видим, что величина напряженности поля диполя убывает с расстоянием от центра диполя как 
, т.е. быстрее, чем напряженность поля точечного заряда. Напряженность поля диполя оказывается пропорциональной величине 
. Если 
- вектор, направленный от отрицательного заряда к положительному, то (Рис.9).
Рис.9
Вектор 
– характеристика диполя, называется электрическим моментом или моментом диполя, дипольным моментом.
Тогда напряженность электрического поля на оси диполя и на перпендикуляре к середине оси диполя можно соответственно определить по формулам:
, (3.5) и 
. (3.6)
Ответ: 
, 
.
Пример 3.4. Вычислить электрическое поле диполя в точке L, положение которой определяется расстоянием 
от точки О и угла 
, который образует прямая OL с осью диполя (Рис.10).
Решение: Чтобы упростить решение, используем следующий прием. Вектор дипольного момента представим суммой двух векторов 
и 
линии OL. 
и 
. Каждый из этих двух диполей в точке L создает поле, определяемое формулами (3.5) и (3.6). При условии
вектор 
можно считать направленным по линии OL (ось диполя 
совпадает с линией OL). Тогда напряженность поля в точке L будет (3.7)
Нетрудно видеть, что если 
или 
, то из уравнения (3.7) получаем уравнение (3.6); а если 
, или 
, получаем уравнение (3.5).
Как видим из рассмотренных примеров, электрическое поле двух связанных разноименных зарядов убывает с расстоянием быстрее, чем поле точечного заряда. Если рассмотреть системы более сложные, например, по два положительных и отрицательных заряда (квадруполь), то его поле будет обратно пропорционально расстоянию в четвертой степени, а для двух квадруполей обратно пропорционально расстоянию в пятой степени. Электрические поля зарядов, связанных в нейтральные системы – короткодействующие.
Пример 3.5. Вычислить напряженность поля, созданного заряженным кольцом, на оси кольца в точке, удаленной от центра кольца на расстояние h. Заряд кольца Q равномерно распределен по всей длине кольца, R – радиус кольца (Рис.11).
Решение: Напряженность поля в точке А можно вычислить как векторную сумму полей, созданных элементарными точечными зарядами, расположенными на малых отрезках 
кольца.
Мысленно разделим кольцо на множество малых элементов , на которых будет размещен заряд 
. Заряд 
можно считать точечным и напряженность поля, созданного этим зарядом в точке А будет 
. Результирующее поле в точке А, определится суммой векторов 
. Сумма двух векторов 
полей, созданных двумя диаметрального противоположными элементами , будет 
, 
.
Как видно из рисунка, этот вектор направлен по оси кольца (по линии, перпендикулярной плоскости кольца и проходящей через его центр). Тогда 
будет иметь такое же направление, модуль этого вектора определим арифметической суммой векторов 
, где
Тогда 
, т. е. 
(3.8)
Ответ. В центре кольца h=0 и E=0. При h>>R имеем 
, что совпадает с электрическим полем точечного заряда q, сосредоточенного в центре кольца.
Пример 3.6. В однородном электрическом поле напряженности находится диполь с электрическим моментом 
. Определить, как будет вести себя диполь в электрическом поле.
Решение. На электрические заряды диполя в однородном поле действуют силы 
. Эти силы равны по величине и направлены противоположно, поэтому образуют пару сил (Рис.12). Момент этой пары равен 
. Учитывая, что - момент диполя, момент сил, действующий на диполь будет 
.
Направлен момент этой пары по оси вращения диполя, т.е. перпендикулярно к и . Величину и направление 
вектора момента пары можно выразить одной формулой 
. (3.9)
Ответ: .
Мы видим, что в однородном электрическом поле на диполь действуют пара сил, которая стремится повернуть диполь таким образом, чтобы векторы и были параллельными, или, говорят, сориентировать диполь по полю.