Метод вырезания узлов

Способы расчета ферм

 

1. Метод вырезания узлов (аналитический и графический).

2. Метод Риттера (метод сечений).

3. Диаграмма Максвелла-Кремоны.

 

1. Предварительно определяем силы опорных реакций, рассматривая равновесие фермы в целом.

Составим систему уравнений равновесия фермы:

,

,

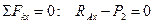Отсюда найдем опорные реакции:

, , .

 

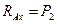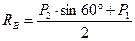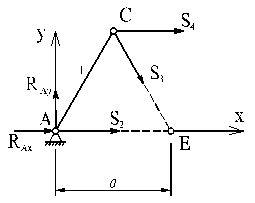
2. Теперь переходим к определению усилий в стержнях. Для сокращения записей пронумеруем стержни согласно рисунку.

 

При вырезании условимся направлять силы реакций в стрежнях фермы (усилия в стержнях) от узлов, предполагая, что все стержни растянуты. Если в результате решения задачи величина усилия окажется положительной, то предположение о растяжении будет подтверждено, а если величина усилия отрицательна, то стержень фактически испытывает сжатие.

 

Решение задачи методом вырезания узлов можно начинать только с тех узлов, в которых сходится по два неизвестных усилия.

 

Вырезаем узел А. Выбрав направление декартовых осей, составляем систему уравнений равновесия узла А.

,

,

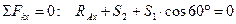Решив эту систему, находим S₁ и S₂.

 

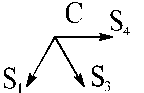Теперь можно перейти к узлу С, так как после определения усилия S₁ в этом узле осталось только две неизвестные силы: S₄ и S₃. Составляем и решаем систему уравнений равновесия узла С.

,

,

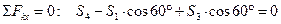откуда находим S₄ и S₃.

 

Теперь рассматриваем равновесие узла В.

,

,

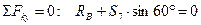находим из этих уравнений S₆ и S₇.

 

Остается определить усилие S₅. Для этого можно рассмотреть равновесие узла D либо Е. Рассмотрим равновесие узла D. Запишем уравнения равновесия узла D в проекциях на декартовы оси.

,

,

Для определения S₅ достаточно одного из этих уравнений – второго.

 

Первое уравнение системы можно использовать для проверки полученных результатов.
Метод Риттера

 

1. Определяем опорные реакции, рассматривая равновесие фермы в целом (см. метод вырезания узлов).

 

2. Мысленно разрезаем ферму на две части, так, чтобы число рассеченных стержней не превышало трех, отбрасываем одну из частей и заменяем действие отброшенной части искомыми усилиями в стержнях, полагая все стержни растянутыми.

 

3. Составляем уравнения равновесия для оставшейся части таким образом, чтобы в каждое уравнение входило только одно неизвестное усилие. Для этого составляем уравнения моментов относительно точек, в которых пересекаются линии действия неизвестных усилий. Если два стрежня параллельны, то составляем уравнение проекций на ось, перпендикулярную к этим стержням.

,

 

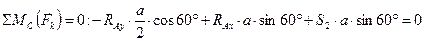
4. Решая каждое из составленных уравнений, находим искомое усилие в стержнях. Если в ответе получим знак минус, то это означает, что стержень сжат, а не растянут.