Равномерное вращение сосуда вокруг вертикальной оси

 

В случае равномерного вращения цилиндрического сосуда вокруг вертикальной оси с угловой скоростью со (рис. 1.5) вектор напряже­ния массовых сил

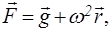(1.51)

а уравнение Эйлера (1.10) имеет вид

dp = r [w² ( xdx +ydy ) – gdz] = r (w ² rdr – gdz). (1.52)

Уравнение свободной поверхности (р = р₀ )

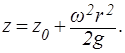(1.53)

Уравнение любой изобарической поверхности (р = const)

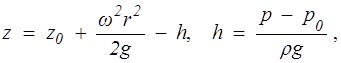(1.54)

где z₀ - координата точки пересечения свободной поверхности с осью вращения.

Изобарические поверхности - параболоиды вращения, ось которых совпадает с осью оz , а вершины смещены вдоль этой оси. Форма изоба­рических поверхностей не зависит от плотности жидкости.

Высота параболоида свободной поверхности (R - радиус сосуда)

 

H = w ²R²/2g. (1.55)

 

Координата z₀ его вершины определяется объемом жидкости в сосу­де. Если начальный уровень в сосуде h₀ , то

z₀ = h - (1.56)

откуда h₁ = h₀ –z₀ = H/2.

 

Закон распределения давления в жидкости

(1.57)

 

Рис. 1.5. Цилиндрический сосуд с жидкостью, вращающийся с постоян­ной угловой скоростью w

 

Изменение давления по вертикали (h — глубина точки под свобод­ной поверхностью) :

 

Р = Р₀ + r gh,

т.е. такое же, как в неподвижном сосуде.