Кольцевой трубопровод

Основной расчетной задачей является определение напора Н в условиях, когда заданы значения расхода в точках отбора (так называемые узловые расходы) Q₁, Q₂, …, Q_n, расположение трубопровода, длины отдельных участков и диаметры всех труб.

Рассмотрим сначала простейший случай (Рис. 6.7), когда трубопровод имеет два узловых расхода: Q₁ (в точке 1) и Q₂ (в точке 2). Определение напора Н в начальном сечении магистрали затруднено тем, что неизвестны ни расход, ни направление потока на замыкающем участке между узлами 1 и 2, в связи с чем неизвестны расходы и на других участках трубопровода.

 

 

 

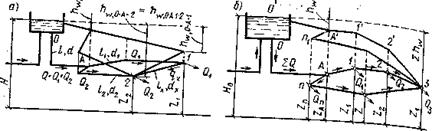
Рис. 6.7. К расчету кольцевого трубопровода.

а – схема кольцевого трубопровода;

б – то же, с двумя узловыми точками.

Если, например, течение происходит от узла 1 к узлу 2, то расход трубопровода на участке А – 1 будет Q₁=q₁+q_x, а если течение направлено от узла 2 к узлу 1, то расход на участке А -1 будет Q₂=q_2-q_x. Поэтому надо предварительно решить вопрос о направлении течения на замыкающем участке трубопровода.

Назовем точкой схода узел, к которому жидкость притекает с двух сторон. Так на рис. 6.8а, такой точкой схода является узел 2, а на рис. 6.8б – узел 1.

 

Рис. 6.8. К определению направления течения на замыкающем участке трубопровода.

 

Положение точки схода определяет направление течения во всем кольце. Потери напора от магистральной узловой точки А до точки схода одинаковы по обоим направлениям «Кольца».

Так, если точкой схода является узел 2:

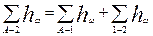. (6.39)

Для этого случая, если пренебречь местными сопротивлениями, можно написать неравенство

и (опуская q_x)

 

,

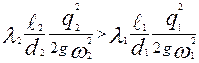или .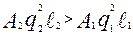

В случае, когда , точкой схода является узел 1.

Таким образов, положение точки схода определяется потерями напора от магистрального узла А до узла 1 и узла 2.

После того как решен вопрос о точке схода, искомый начальный напор определяется путем вычисления в каком – нибудь одном направлении потерь напора до точки схода от начального сечения трубопровода. Например, если для схемы, показанной на рис. 6.7., точкой схода является точка 2, то

.

 

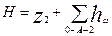7. Истечение жидкости через отверстия и насадки

Исследование истечения жидкости из отверстий и насадков имеют большое практическое значение, т.к. результаты их находят применение при решении многих технических задач.

Для практики наибольший интерес представляет задача о связи между давлением (напором) в каком – либо резервуаре и расходом (или скоростью) струи, вытекающей из отверстия в стенке или в дне резервуара.

 

 

7.1.Истечение жидкости из отверстий в тонкой стенке

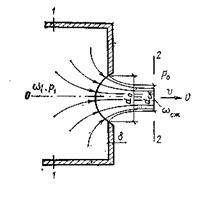Рассмотрим вначале истечение жидкости из круглого отверстия, диаметром d₀ в вертикальной тонкой стенке сосуда (рис.7.1). Стенку можно считать тонкой, если ее толщина 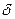<0.2 d₀. Давление в сосуде полагаем постоянным (движение установившееся) и равным р_1.

Рис. 7.1. Истечение жидкости и отверстия в тонкой стенке.

 

Истечение происходит в атмосферу, т.е. наружное давление р₀; площадь отверстия 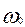, площадь сечения сосуда. Экспериментально установлено, что по выходе из отверстия струя сжимается и на расстоянии 0,5 диаметра отверстия струя приобретает наименьшую площадь (при диаметре )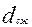

.

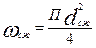Коэффициент сжатия струи (7.1)

зависит от отношения 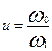, (7.2)

называемого степенью сжатия.

В обычных условиях при истечении воды из малых отверстий в больших резервуарах коэффициент сжатия струи находится в пределах =0,61-0,63.

Для определения скорости истечения жидкости запишем уравнение Бернулли для сечений 1-1 и 2-2, причем сечение 2-2 проведем через наиболее сжатый участок струй .

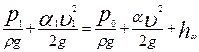. (7.3)

Давление в сжатом сечении струи р можно принять равным атмосферному, т.е. р₀, т.к. истечение происходит в атмосферу.

Потери напора между сечениями 1-1 и 2-2 определяются формулой Вейсбаха

 

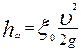, (7.4)

где - коэффициент сопротивления отверстия.

Принимая 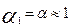. (на основании опытных данных), получим:

.

Решая это уравнение относительно , находим

. (7.5)

Разделив обе части равенства на , получим

.

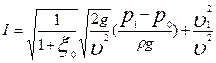Принимая во внимание, что 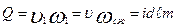, преобразуем записанную выше формулу к виду

(7.6)

имея в виду, что

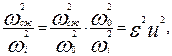(7.7)

и возведя обе части уравнения (7.6) в квадрат, получим:

откуда имеем

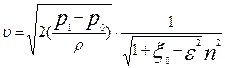. (7.8)

Введем обозначение

 

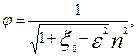(7.9)

где - коэффициент скорости истечения.

Тогда получаем 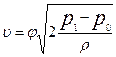(7.10)

 

При истечении из малых отверстий ()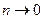

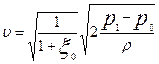. (7.11)

При малом влиянии вязкости =0; =1, вместо формулы (7.11) получаем

. (7.12)

При истечении воды и воздуха обычно принимают =0,97-0,98; =0,06, т.е. всего около 2-3% располагаемой разности давлений затрачивается на преодоление сопротивлений.

Расход жидкости, выходящей из отверстия, находим по формуле

.

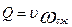Подставляя вместо и их значения, имеем

.

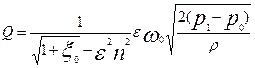Введем обозначение

(7.13)

где - коэффициент расхода отверстия.

Тогда получим формулу для определения расхода

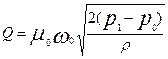. (7.14)

При истечении из малых отверстий (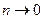) из формулы (7.13) имеем

. (7.15)

При истечении воды и воздуха для рассматриваемого случая =0,6.