Идеальной жидкости
Интегрирование дифференциальных уравнений равновесия
Умножая уравнения (2.7) соответственно на dx, dy и dz и складывая их, получим
. (2.8)
Поскольку р = f(x,y,z), выражение в скобках в правой части уравнения (2.8) есть полный дифференциал гидростатического давления, следовательно,
(Xdx + Ydy + Zdz)=dp. (2.9)
Уравнение (2.9) есть основное уравнение гидростатики в дифференциальной форме.
Проинтегрируем уравнение (2.9) для случая, когда жидкость заключена в вертикальном цилиндрическом сосуде и находится в покое под действием силы тяжести и внешнего давления на ее свободной поверхности (рис. 3).
Рис.3
Горизонтальная плоскость XOY называется плоскостью сравнения.
Для рассматриваемого случая, составляющие единичной силы тяжести по координатным осям будут равны:
Х= 0; Y= 0; Z= - g, и отсюда
dp= -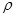
g·dz. (2.10)
p= -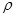g·Z+C. (2.11)
При р = р0 и Z = Z0
C = p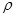0 + gZ0,
поэтому уравнение (2.11) примет вид
p = -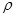g · Z + р0+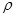gZ0 , (2.12)
или
p = p0 +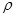g(Z0 -Z) = p0 +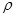gh, (2.13)
p = p0 +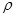gh, (2.14)
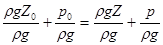, (2.15)
. (2.16)
Уравнения (2.14) и (2.15) – это две разновидности основного уравнения гидростатики.
Уравнение (2.14) является математическим выражением закона распределения гидростатического давления в жидкости: величина гидравлического давления в некоторой точке, погруженной на глубину h относительно свободной поверхности, равна сумме внешнего давления на свободную поверхность жидкости р0 и давления от веса столба жидкости с площадью основания, равной единице, и высотой, равной глубине погружения h рассматриваемой точки.
Помимо этого уравнение (2.14) показывает, что внешнее давление р0, которое действует на поверхность жидкости, передается всем точкам жидкости без изменения. В этом заключается суть закона Паскаля.