Поле скоростей и ускорений
Движение сплошной среды характеризуется прежде всего скоростями ее частиц. В каждый момент времени они имеют определенную по величине и направлению скорость.
Если поле скоростей и давлений остается неизменным во времени, то движение называется установившимся.
В случае установившегося движения давление и скорость могут изменяться при перемещении частицы жидкости из одного положения в другое, но в данной неподвижной относительно русла точке давление и скорость являются функциями только координат.
p=f1(x,y,z)
v=f2(x,y,z0
В случае неустановившегося течения давления и скорость зависят как от координат, так и от времени.
P=F1(x,y,z,t) V=F2(x,y,z,t)
В практике часто пользуются понятиями средн. скоростей. Обычно усреднение скорости производится либо по времени, либо по площади некоторого сечения потока.
Среднее значение величины скорости за промежуток времени t0 представляет собой интеграл:
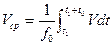
Средняя величина скорости по некоторой площади S определятся как
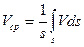
Вектор ускорения жидкой частицы, движущейся со скоростью V является индивидуальной производной по времени от вектора скорости

Т.к. вектор скорости в общем случае зависит от времени и координат
V=V(x,y,z.t), то по правилу дифференцирования сложной функции найден
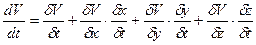
Т.к. производные от координат движущейся точки по времени есть соответствующие проекции скоростей, т.е.
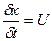 ;
; 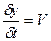 ;
; 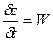
Получим 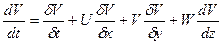
В проекциях на оси координат x,y,z это уравнение будет иметь вид:
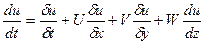

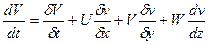
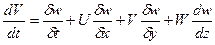
Первое слагаемое первой части равенства выражаем изменение скорости во времени в некоторой фиксированной точке пространства, т.е местное изменение и поэтому называется локальной составляющей ускорения. Остальные слагаемые характеризуют изменение скорости частицы при ее перемещении и называются конвективными составляющими ускорения.
При установившемся движении локальное ускорение всегда равно 0. при неустановившемся оно может обращаться в 0 лишь тогда, когда в данной точке скорость имеет max или min значение во времени.
Конвективное ускорение может быть при установившемся и неустановившемся движениях. Оно обращается в 0 лишь тогда, когда средняя скорость не зависит от координат.
Векторные линии и траектории
Векторной линией в поле векторов называется линия, в каждой точке которой в данный момент времени вектор касателен к ней.
Совокупность векторных линий, проходящих через все точки некоторого контура, образует векторную поверхность.
Если рассматривать движение жидкой частицы во времени, то линия, по которой двигалась частица в некоторый момент времени называется траекторией.
Траектории частиц жидкости при установившемся течении являются неизменными во времени.
При неустановившемся течении траектории различных частиц, проходящих через данную точку пространства, могут иметь разную форму. Поэтому для рассмотрения картины течения, возникающей в каждый момент времени, вводится понятие линии тока.
Линией тока называется кривая, в каждой точке которой вектор скорости в данный момент времени направлен по касательной.
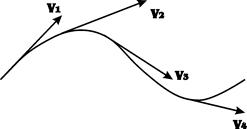
Для установившегося движения тока, совпадает с траекторией частицы и не изменяет своей формы с течением времени.
Если в движущейся жидкости взять бесконечно малый замкнутый контур и через все его точки провести линии тока, то образуется трубчатая поверхность называемая трубкой тока.
Часть потока, заключенная внутри трубки тока, называется элементарной струйкой.
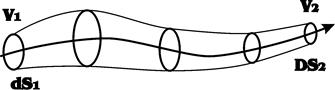
При стремлении поперечных сечений размеров струйки к 0 она в пределе стягивается в линию тока.
Живым сечением или просто сечением потока, называется в обще случае поверхность в пределах потока, проведенная нормально к линиям тока. Далее будем рассматривать в потоках такие участки, в которых струйки можно считать параллельными, и следовательно, живые сечения плоскими.
Расходом называется количество жидкости , протекающей через живое сечение потока (струйки) в единицу времени.
Для элементарной струйки, имеющей бесконечно малые площадки сечений, можно считать истинную скорость V одинаковой во всех точках каждого сечения, тогда элементарный расход, проходящий через площадку dS выразится так dS = VdS [м3/c]
Для потока конечных размеров в общем случае скорость имеет различное значение в разных точках сечения, поэтому расход надо определять как сумму элементарных расходов струек.
Q=SVdS
Основываясь на законе сохранения вещества, на предположение о сплошности (неразрывности) течения и на непроницаемости трубки тока можно утверждать, что расходство всех сечениях элементарной струйки одинаков.
dQ=V1dS1=V2dS2=const – (вдоль струйки)
Для потока конечных размеров, ограниченного непроницаемыми стенками следует ввести средние скорости
Q=VсрS1=VсрS2=const – (вдоль потока)
Основное уравнение гидродинамики
Из последнего уравнения следует, что средние скорости в потоке несжимаемой жидкости обратно пропорциональных площадям живых сечений
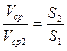
ЛЕКЦИЯ 4 Основные уравнения динамики жидкости.
Закон сохранения массы и уравнения неразрывности
Закон сохранения массы для изолированной системы выражается в том, что масса m такой системы остается постоянной во время движения. Следовательно, полная производная от массы по времени равно 0.
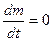
Используя закон сохранения массы для элементарного объема получим:
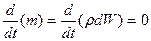
После дифференцирования будем иметь
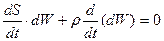
Второе слагаемое деленное на ρdW есть величина относительного изменения объема dW, равная
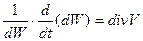
сумма диагональных компонент тендора скоростей дифференциальный
/Тогда получим
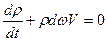 Уравнение неразрывности, является выражением закона сохранения массы.
Уравнение неразрывности, является выражением закона сохранения массы.
Если жидкость несжимаема ,то есть ρ=const, то уравнение неразрывности примет вид:
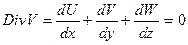
2, Закон сохранения количества движения (импульса). Дифференциальные уравнения динамики жидкости в напряжениях.
Закон сохранения импульса можно сформулировать так:
« Разность векторной производственной от количеств движения жидкого объема и всех внешних сил, приложенных к нему, равна нулю во все время движения».
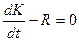
Для конечного объема жидкости W с поверхности S закон сохранения импульса можно записать

Путем математических преобразований получаем закон сохранения импульса в векторной форме:
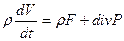 , где
, где 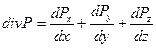
Закон сохранения импульса в проекциях на оси координат можно записать:
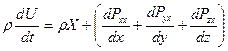
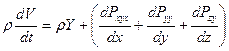
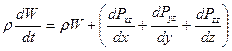
Лекция 5
Динамика идеальной и вязкой жидкости.
В целях упрощения постановки задач при изучении законов движения жидкости создана модель идеальной жидкости.
Идеальной жидкостью называется воображаемая жидкость, которая характеризуется полным отсутствием вязкости и абсолютной неизменяемостью объема при изменении давления.
Дифференциальные уравнения движения идеальной жидкости можно получить из дифференциальных уравнений покоя (смотри Гидростатику), если согласно принципу Даламбера ввести в эти уравнения силу инерции, отнесенную к единице массы движущейся жидкости.
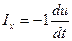
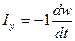

 - I x , Iy , Iz,проекции силы инерции, равной произведению массы на ускорение, на оси координат Ix = ρ dx dy dz dUx/ dt
- I x , Iy , Iz,проекции силы инерции, равной произведению массы на ускорение, на оси координат Ix = ρ dx dy dz dUx/ dt
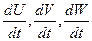 проекции ускорений на оси координат.
проекции ускорений на оси координат.
Сила инерции направлена в сторону противоположную ускорению, поэтому она входит со знаком минус.
Вводя силу инерции в дифференциальное уравнение равновесия (уравнение Эйлера) получим:
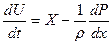


Уравнение движения Эйлера для идеальной жидкости.
Граничные условия:
1. Непроницаемость стенки.
2. Безотрывное течение вдоль стенки
«Полное ускорение частицы вдоль координатной оси складывается из ускорения от массовых сил и от ускорения сил давления».
В векторной форме уравнение имеет вид

Переходя от идеальной жидкости к реальной (вязкой) жидкости, в полученные уравнения вводятся дополнительные слагаемые, учитывающие силы трения, отнесенные к единице массы жидкости.
Такая операция приводит нас к системе трех уравнений, называемых уравнениями Навье – Стокса.



Последнее дополнительное слагаемое учитывает силы трения. Выражения в скобках представляют собой соответствующие суммы вторых частных производных от U,V,W по координатам x,y, z.
Для получения конкретных решений при интегрировании системы уравнений должны быть заданы граничные условия:
1. Условие прилипания частиц к твердой стенке а) равенство 0 скорости на неподвижной стенке или б) совпадение скоростей частиц жидкости со скоростями точек движущейся твердой поверхности.
2. В случае внешнего обтекания: задание скорости во внешнем потоке. В случае движения в трубе: задание расхода.
3. Задание давления в какой-либо одной точке потока
4. В векторном виде
5.  , где символ ММ обозначает вектор с проекциями VU, VV, VW .
, где символ ММ обозначает вектор с проекциями VU, VV, VW .