БИБЛИОТЕКА ВЫСШЕЙ ШКОЛЫ
Классификация кривых второго порядка.
Рекомендуемая литература
II. УЧЕБНО-МЕТОДИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ДИСЦИПЛИНЫ
Literatur
1. Маслова 2008: 19 – 59.
2. Гончарова 2005: 3 - 50.
3. Бахтин 1986: 474.
4. Schendels 1988: 402 - 403.
5. Девкин В.Д. Диалог. – М.: Высшая школа, 1981. – С. 5 – 8.
а) Основная литература
Admoni, W. Der deutsche Sprachbau [Текст] / W. Admoni. – M.–Л.:Просвещение, 1966 (L., 1972, M., 1986). – 384 с.
Moskalskaja, O.I. Grammatik der deutschen Gegenwartssprache [Текст] / О.I. Moskalskaja. – M.: Hochschule, 1975. – 384 S.
б) Дополнительная литература
Абрамов, Б.А.Теоретическая грамматика немецкого языка [Текст] / Б.А.Абрамов. – М.: Владос, 1999. – 246 c.
Адмони, В.Г Синтаксис современного немецкого языка [Текст] / В.Г. Адмони. – Л.: Наука, 1973. – 366 с.
Амзаракова И.П., Савченко В.А. Стилистика: выразительные средства немецкого языка: учебное пособие [Текст] / И.П. Амзаракова, В.А. Савченко. – Абакан: Изд-во ХГУ им. Н.Ф. Катанова, 2009. – 140 с.
Бахтин М.М. Проблема текста в лингвистике, филологии и других гуманитарных науках. Опыт филологического анализа // Литературно-критическая статья / Сост. С. Бочаров и В. Кожинов [Текст] / М.М. Бахтин. – М.: Худож. лит., 1986. – 546 с.
Гончарова Е.А. Интерпретация текста. Немецкий язык: Учеб. пособие [Текст] / Е.А. Гончарова, И.П. Шишкина. – М.: Высшая школа, 2005. – 368 с.
Гулыга, Е.В. Теория сложноподчиненного предложения в современном немецком языке [Текст] / Е.В. Гулыга. – M.: Высшая школа, 1971. – 206 с.
Гулыга, Е.В. Грамматико-лексические поля в современном немецком языке [Текст] / Е.В. Гулыга, Е.И. Шендельс. – М.: Просвещение, 1969. – 184 с.
Малинович, Ю.М. Экспрессия и смысл предложения: Проблемы эмоционально-экспрессивного синтаксиса [Текст] / Ю.М. Малинович. – Иркутск: Изд-во Иркутского университета, 1989. – 215 с.
Маслова, В.А. Современные направления в лингвистике: учебное пособие для студентов высших учебных заведений [Текст] / В.А. Маслова. – М.: Академия, 2008. – 272 с.
Михайлов,Л.М. Коммуникативная грамматика немецкого языка. // Учебник для институтов и факультетов иностранных языков [Текст] / Л.М. Михайлов. – М.: Высшая школа, 1994. – 256 с.
Москальская, О.И. Проблемы системного описания синтаксиса [Текст] / О.И.Москальская. – М.: Высшая школа, 1984. – 175 с.
Степанова, М.Д. Части речи и проблема валентности в современном немецком языке [Текст] / М.Д. Степанова, Г. Хельбиг. – М.: Высшая школа, 1978. – 258 с.
Филичева, Н.И. О словосочетаниях в современном немецком языке [Текст] / Н.И. Филичева. – М.: Высшая школа, 1969. – 253 с.
Харитонова, И.Я. Теоретическая грамматика немецкого языка. Синтаксис [Текст] / И.Я. Харитонова. – Киев, 1976. – 179 с.
Шендельс, E.И. Mногозначность и синонимия в грамматике [Текст] / Е.И. Шендельс. – M.: Высшая школа, 1970. – 202 с.
Döring, B. Übungstexte zur deutschen Grammatik [Text] / B. Döring, G. Hänse u.a. – Leipzig, 1983. – 237 S.
Duden-Grammatik [Text] 5.Auflage. – Dudenverlag Mannheim, Leipzig, Wien, Zürich, 1995. - 504 S.
Erben, J. Abriss der deutschen Grammatik [Text] – Berlin, 1965. – 458 S.
Erben, J. Deutsche Grammatik. Ein Abriss [Text]. – München, 1972. – 316 S.
Faulseit, D. Stilistische Mittel und Möglichkeiten der deutschen Sprache [Text] // D. Faulseit, G. Kühn. – VEB Bibliographisches Institut Leipzig, 1975. – 286 S.
Helbig, G. Deutsche Grammatik. Ein Handbuch für den Ausländerunterricht [Text] / G. Helbig, J. Buscha. – Leipzig, 1975. – 316 S.
Helbig, G. Wörterbuch zur Valenz und Distribution der deutschen Verben [Text] / G. Helbig, W. Schenkel. – Leipzig 1977. - 458 S.
Moskalskaja, O.I. Grammatik der deutschen Gegenwartssprache [Text] – M., 1971 (1975, 1983).
Schendels E. Deutsche Grammatik [Text] / E. Schendels. - М.: Высшая школа, 1988. – 489 с.
Schischkowa, L.W., I.I. Seminare in der theoretischen Grammatik der deutschen Gegenwartssprache [Text] / L.W. Schischkowa, I.I. Meiskina. – M., 1984. – 167 S.
Schmidt,W. Grundfragen der deutschen Grammatik [Text] / W. Schmidt. – Berlin, 1967 (1973).
Sommerfeldt, K.-E., Schreiber H. Wörterbuch zur Valenz und Distribution der deutschen Adjektive [Text]. – Leipzig, 1975. - 435 S.
Sommerfeldt, K.-E., Schreiber H. Wörterbuch zur Valenz und Distribution der deutschen Substantive [Text]. – Leipzig, 1977. - 432 S.
Starke, G. Entwicklungstendenzen in der deutschen Gegenwartssprache [Text] / G. Starke // Deutschunterricht, 1986, №2. – S. 604 - 609.
Важной задачей аналитической геометрии является исследование общего уравнения линии второго порядка и приведение его к простейшим (каноническим) формам.
Пусть дано общее уравнение линии второго порядка:
 . (1)
. (1)
Задача состоит в том, чтобы перейти, от так сказать, «случайной» системы координат к «естественной» для данной кривой.
Уточним предъявляемые требования:
1. нужно добиться, чтобы в группе старших членов исчез член с произведением текущих координат;
2. чтобы число членов первой степени стало меньшим (если возможно, - совсем их уничтожить);
3. кроме того, если возможно, уничтожить свободный член.
Уравнение, получаемое при соблюдении этих требований, называется каноническим.
Покажем на примерах, как следует выполнять необходимые действия, чтобы привести данное уравнение к каноническому виду.
Рассмотрим теперь пример полного преобразования уравнения линии 2 – го порядка с помощью параллельного переноса и поворота системы координат.
Привести к каноническому виду уравнение линии. Выполнить построение линии:

Прежде всего постараемся упростить выражение при помощи параллельного переноса координатных осей. Перенесём начало координат в точку  , которую пока будем считать произвольной. Получим соответствующее преобразование координат по формулам (2):
, которую пока будем считать произвольной. Получим соответствующее преобразование координат по формулам (2):  . Получим:
. Получим:

С помощью параллельного переноса мы должны избавиться от линейных слагаемых в уравнении, т.е. приравниваем нулю:

Эти равенства должны выполняться для всех  , т.е. получаем систему:
, т.е. получаем систему:
 Тогда:
Тогда:  или
или 

Таким образом, перенос системы координат необходимо произвести в точку  . При этом получим уравнение:
. При этом получим уравнение:

Чтобы избавиться от смешанного произведения  , выполним поворот системы координат по формулам (4):
, выполним поворот системы координат по формулам (4):


Нам необходимо убрать смешанное произведение, поэтому группируем соответствующие коэффициенты и приравниваем их к нулю:
 Учитывая тригонометрические формулы, получаем:
Учитывая тригонометрические формулы, получаем:
 .
.
Перепишем уравнение линии, с учётом того, что смешанного произведения в уравнении не осталось:
 или,
или,  и тогда:
и тогда:  и, окончательно,
и, окончательно, 
Получили каноническое уравнение эллипса с полуосями 
 . Построим данную линию:
. Построим данную линию:







1 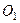

 1
1 
Рассмотрим ещё примеры: Пример 1. Построить следующую линию: 
Из уравнения видим, что должно быть выполнено:  . Возведём равенство в квадрат:
. Возведём равенство в квадрат:  . Тогда
. Тогда  Получено уравнение окружности с центром в точке
Получено уравнение окружности с центром в точке  радиуса 4.
радиуса 4.







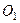
С учётом условия  , мы получаем нижнюю часть окружности.
, мы получаем нижнюю часть окружности.
Пример 2. Построить линию: 
 . Ограничение:
. Ограничение:  Возведём последнее равенство в квадрат
Возведём последнее равенство в квадрат  . Это уравнение параболы с вершиной в точке
. Это уравнение параболы с вершиной в точке  .
.  . Построим линию:
. Построим линию:





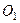 2
2 
-1 

Ввиду условия  , выбираем правую ветку параболы.
, выбираем правую ветку параболы.
Лекция №
§ 7 ПОЛЯРНАЯ СИСТЕМА КООРДИНАТ.
Полярная система координат на плоскости определяется заданием некоторой точки  , называемой полюсом; исходящего из этой точки луча
, называемой полюсом; исходящего из этой точки луча  , называемого полярной осью и масштабной единицей
, называемого полярной осью и масштабной единицей  для измерения длин.
для измерения длин.
Для произвольной точки  плоскости координатами в данной системе координат называют полярный радиус
плоскости координатами в данной системе координат называют полярный радиус  , вычисленный в масштабных единицах, и полярный угол
, вычисленный в масштабных единицах, и полярный угол  между осью
между осью  и радиус – вектором
и радиус – вектором  , т.е.
, т.е.  ,
,






 1
1 

Чаще всего предполагают, что  или
или  Иногда допускаются отрицательные значения для
Иногда допускаются отрицательные значения для  , но при этом соответствующие значения откладываются на продолжении луча.
, но при этом соответствующие значения откладываются на продолжении луча.
 Установим связь между полярными координатами точки и её декартовыми координатами. Для этого совместим начало декартовой системы координат с полюсом полярной системы координат, а ось
Установим связь между полярными координатами точки и её декартовыми координатами. Для этого совместим начало декартовой системы координат с полюсом полярной системы координат, а ось  - с полярной осью:
- с полярной осью:








Используя тригонометрические формулы легко получаются формулы переходаот декартовых координат к полярным:
 (1)
(1)
и формулы обратного перехода от полярных координат к декартовым:
 (2)
(2)
Чаще всего эти формулы используются комбинированно.
Окружность  в полярной системе координат имеет уравнение
в полярной системе координат имеет уравнение  , или
, или  , тогда данная линия имеет вид:
, тогда данная линия имеет вид:






 Аналогичным образом, окружность
Аналогичным образом, окружность  имеет в полярных координатах уравнение,
имеет в полярных координатах уравнение,  и соответствующий рисунок линии выглядит следующим образом:
и соответствующий рисунок линии выглядит следующим образом:





Окружность  с центром в начале координат в полярных координатах имеет уравнение
с центром в начале координат в полярных координатах имеет уравнение  или
или  .
.
Если задано уравнение линии в полярных координатах  , то чтобы построить данную линию в полярной системе координат, заполняют таблицу значений этой функции в точках, вычисленных для значений аргумента
, то чтобы построить данную линию в полярной системе координат, заполняют таблицу значений этой функции в точках, вычисленных для значений аргумента  , причём, чем больше
, причём, чем больше  , тем точнее будет построение линии.
, тем точнее будет построение линии.
Пример 1. Построить линию:  .
.
Заполнить таблицу значений данной функции:

| 
| 
| 
| 
| 
| 
| 
| 
| |

|

| 
| 
| 
| 
| 
| 
| 
| 
|

|
Построим данную линию


















При построении линии в полярных координатах можно поступать и иначе, а именно, используя свойства соответствующих функций.
Пример 2. Пусть дано уравнение  . Так как
. Так как  , то максимальное значение данная функция принимает при
, то максимальное значение данная функция принимает при  -
-  ; минимальное значение будет в точке
; минимальное значение будет в точке  -
-  .
.
 Так как
Так как  чётная функция, то
чётная функция, то  также чётная функция и поэтому соответствующая линия симметрична относительно полярной оси. Таким образом, получаем линию:
также чётная функция и поэтому соответствующая линия симметрична относительно полярной оси. Таким образом, получаем линию:







Эту линию называют кардиоидой, имея ввиду её форму.
Пример 3. Построить линию  .
.
Достаточно построить данную линию на промежутке  , так как период данной функции равен
, так как период данной функции равен  . Учитывая, что
. Учитывая, что  в промежутке
в промежутке  , следовательно
, следовательно  . После этого, учитывая периодичность функции, можно построить ещё две части этой линии, которые получаются при
. После этого, учитывая периодичность функции, можно построить ещё две части этой линии, которые получаются при  .
.










В заключение параграфа напишем уравнение эллипса, гиперболы и параболы в полярных координатах.
 Пусть
Пусть  - дуга эллипса, гиперболы или параболы:
- дуга эллипса, гиперболы или параболы:












Совместим фокус  с полюсом, а ось симметрии - с полярной осью. Точка
с полюсом, а ось симметрии - с полярной осью. Точка  выбрана так, что
выбрана так, что  . По свойству директрисы:
. По свойству директрисы:  . Пусть
. Пусть  ,
,  или
или 
 . Для точки
. Для точки  имеем
имеем  . Тогда,
. Тогда,  . Обозначив
. Обозначив  , получим
, получим  . Следовательно,
. Следовательно,  , отсюда:
, отсюда:  , или
, или  . Окончательно получаем уравнение:
. Окончательно получаем уравнение:
 . (3)
. (3)
При  - это уравнение эллипса; при
- это уравнение эллипса; при  - это уравнение одной ветки гиперболы; при
- это уравнение одной ветки гиперболы; при  - это уравнение параболы.
- это уравнение параболы.
Пример 4. Построить линию  и записать её уравнение в декартовой системе координат.
и записать её уравнение в декартовой системе координат.
Можно произвести построение данной линии непосредственно в полярной системе координат, как в примере 1. Но в данном случае, учитывая формулу (3), это уравнение эллипса с  . Поэтому более удобно сначала перейти к декартовым координатам и только после этого построить линию (менее трудоёмкий вариант решения). Преобразуем уравнение линии:
. Поэтому более удобно сначала перейти к декартовым координатам и только после этого построить линию (менее трудоёмкий вариант решения). Преобразуем уравнение линии:  . Используя формулы (1) и (2), получаем:
. Используя формулы (1) и (2), получаем:

 (4) обе части полученного равенства возведём в квадрат:
(4) обе части полученного равенства возведём в квадрат:


Получено каноническое уравнение эллипса:

Его центр симметрии  , полуоси
, полуоси 
 Построим данную линию:
Построим данную линию:



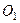 4 5
4 5 
Уравнение вида  также определяет линию 2 – го порядка, но в этом случае сдвиг точки
также определяет линию 2 – го порядка, но в этом случае сдвиг точки 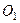 происходит влево, а уравнение
происходит влево, а уравнение  приводит к смещению линии по оси
приводит к смещению линии по оси 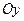 .
.
ВТ. Крысько