КОНТРОЛЬНЫЙ ЛИСТОК.
Контрольный листок (или лист) -инструмент для сбора данных и автоматического их упорядочения для облегчения дальнейшего использования собранной информации. Контрольный литок - бумажный бланк, на котором заранее напечатаны контролируемые параметры, соответственно которым можно заносить данные с помощью пометок или простых символов.
Число различных конкретных контрольных листков исчисляется сотнями, и в принципе для каждой конкретной цели может быть разработан свой листок. Но принцип их оформления остается неизменным: наименование контролируемого параметра, место измерений, ответственный исполнитель, время проведения измерений, порядок регистрации данных. Пример оформления контрольного листка приведен в таблице 6.1, а результаты обработки данных контрольного листка в таблице 6.2.
Таблица 6.1.
Измерение пробивного напряжения диэлектрических
слоев МОП - структур на измерительной установке.
Каждое значений пробивного напряжения отмечайте так: I
Время: 22-27 февраля 1999 г.
Лаборант: Иванов И.И.
| Х | Количество наблюдений | m | X | Количество наблюдений | m |
| / | ///////// | ||||
| / | //////// | ||||
| / | ////////////// | ||||
| / | ////////// | ||||
| / | ////////// | ||||
| // | / | ||||
| // | /////// | ||||
| // | ////// | ||||
| ///////// | ///// | ||||
| ////////// | /// | ||||
| /// | ///// | ||||
| /////// | / | ||||
| ////// | // | ||||
| ////// | / | ||||
| ///////////////// | // | ||||
| ////// | / |
Данные, полученные на основании контрольного листка, представляют собой первичный статистический материал, подлежащий обработке, осмыслению и научному анализу. Упорядоченное представление данных называется ранжированием (таблица 6.2.). Для получения статистического ряданеобходимо не только ранжировать статистический материал, но и подвергнуть его дополнительной обработке, объединив одни и те же значения в интервалы или группы. За величину интервала,как правило, принимают его середину, т.е. центральное значение.
Удобно представлять статистический материал числовыми значениями, которые до некоторой степени отражают существенные характеристики статистического ряда - характеристики положения и рассеивания случайной величины. Важнейшими характеристиками положения являются: средняя арифметическая величина, мода и медиана. Мода - значение случайной величины, которое наиболее часто встречается в данном ряду (в примере мода равна 196). Медиана - значение параметра, которое делит упорядоченный ряд на две равные по объему группы.
Для отображения рассеивания в математической статистике применяют ряд характеристик. Размах R -разность между наибольшим и наименьшим значениями наблюдаемой случайной величины.
Выборочная дисперсия (s2)показывает, как тесно группируются отдельные значения вокруг средней арифметической или как они рассеиваются вокруг этой средней - сумма квадратов отклонений отдельных значений от средней арифметической, деленную на число наблюдений, уменьшенное на единицу. Корень квадратный из выборочной дисперсии называется выборочным стандартным отклонением (s). Отношение стандартного отклонения к средней арифметической, выраженное в процентах, называется коэффициентом вариации (V), который показывает относительное колебание отдельных значений около средней арифметической.
Таблица 6.2.
Интервальный ряд распределения пробивных напряжений диэлектрических слоев МОП - структур
| Интервал | Середина интервала | Частота mi | Относительная частота wi,% | Накопленная частота Smi | Относительная накопленная частота S mi |
| 176,5...179,4 | 0,6 | 0,6 | |||
| 179,5...182,4 | 1,9 | 2,5 | |||
| 182,5...185,4 | 3,1 | 5,6 | |||
| 185,5...188,4 | 13,1 | 18,1 | |||
| 188,5...191,4 | 10,0 | 28,7 | |||
| 191,5...194,4 | 18,1 | 46,8 | |||
| 194,5...197,4 | 19,4 | 66,2 | |||
| 197,5...200,4 | 13,1 | 79,3 | |||
| 200,5...203,4 | 11,4 | 90,7 | |||
| 203,5...206,4 | 5,6 | 96,3 | |||
| 206,5...209,4 | 3,1 | 99,4 | |||
| 209,5...212,4 | 0,6 | 100,0 |
Математической ожиданиеиграет роль характеристики положения случайной величины в генеральной совокупности, и поэтому его иногда называют генеральным средним арифметическим значением случайной величины или центром группирования значений случайной величины в генеральной совокупности. Математическое ожидание рассчитывается с учетом вероятности попадания в выборку отдельных значений контролируемого параметра.
Дисперсиюслучайной величины Х в генеральной совокупности (s2) рассчитывают по формуле:

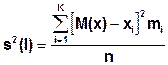
где М(х) - генеральное среднее арифметическое значение случайной величины х;
к - количество интервалов;
хi- величина интервала;
n - количество измерений;
mi - частота в интервале;
i - номер интервала.
Чаще на практике вместо дисперсии применяют стандартное отклонение s(х), которое вычисляется как корень квадратный из величины дисперсии.
Важнейшим этапом, предшествующим принятию решения при управлении процессом, является определение закона распределения случайной величины по выборочным данным. Наиболее часто встречается Гауссовский закон распределения.В математической статистике применяется способ оценки диапазона возможных значений случайной величины известный под названием правила трех сигм. Согласно этому правилу в диапазоне М(х) s находится 68,27% всех наблюдений, в диапазоне М(х) 2s - 95,45%, в диапазоне М(х) 3s - 99,73%.