Быстрая сортировка

Сортировка методом пузырька

Это наиболее простой метод сортировки. Его сложность N². Эффективен, если исходные данные в некоторой мере упорядочены, например, если в отсортированный массив добавляется небольшое количество новых данных.

int t,k=0;

char flag;

do

{

flag = 0;

for(int i=0;i<N-1-k;i++)

if (m[i]>m[i+1]) {t=m[i];m[i]=m[i+1];m[i+1]=t;flag=1;}

k++;

}while(flag);

"Быстрая сортировка", хоть и была разработана более 40 лет назад, является наиболее широко применяемым и одним их самых эффективных алгоритмов.

Метод основан на подходе "разделяй-и-властвуй". Общая схема такова:

из массива выбирается некоторый опорный элемент a[i],

запускается процедура разделения массива, которая перемещает все ключи, меньшие, либо равные a[i], влево от него, а все ключи, большие, либо равные a[i] - вправо,

теперь массив состоит из двух подмножеств, причем левое меньше, либо равно правого,

для обоих подмассивов: если в подмассиве более двух элементов, рекурсивно запускаем для него ту же процедуру.

В конце получится полностью отсортированная последовательность.

Рассмотрим алгоритм подробнее.

Разделение массива

На входе массив a[0]...a[N] и опорный элемент p, по которому будет производиться разделение.

Введем два указателя: i и j. В начале алгоритма они указывают, соответственно, на левый и правый конец последовательности.

Будем двигать указатель i с шагом в 1 элемент по направлению к концу массива, пока не будет найден элемент a[i] >= p. Затем аналогичным образом начнем двигать указатель j от конца массива к началу, пока не будет найден a[j] <= p.

Далее, если i <= j, меняем a[i] и a[j] местами и продолжаем двигать i,j по тем же правилам...

Повторяем шаг 3, пока i <= j.

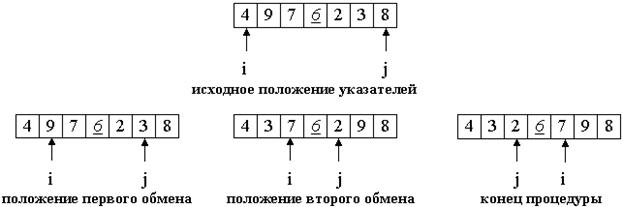
Рассмотрим работу процедуры для массива a[0]...a[6] и опорного элемента p = a[3].

Теперь массив разделен на две части: все элементы левой меньше либо равны p, все элементы правой - больше, либо равны p. Разделение завершено.

 

Реализация на Си.

template<class T>

void quickSortR(T* a, long N) {

// На входе - массив a[], a[N] - его последний элемент.

long i = 0, j = N; // поставить указатели на исходные места

T temp, p;

p = a[ N/2]; // центральный элемент

// процедура разделения

do {

while ( a[i] < p ) i++;

while ( a[j] > p ) j--;

if (i <= j) {

temp = a[i]; a[i] = a[j]; a[j] = temp;

i++; j--;

}

} while ( i<=j );

 

// рекурсивные вызовы, если есть, что сортировать

if ( j > 0 ) quickSortR(a, j);

if ( N > i ) quickSortR(a+i, N-i);

}

Каждое разделение требует, очевидно, Theta(n) операций. Количество шагов деления(глубина рекурсии) составляет приблизительно log n, если массив делится на более-менее равные части. Таким образом, общее быстродействие: O(n log n), что и имеет место на практике.

Однако, возможен случай таких входных данных, на которых алгоритм будет работать за O(n2) операций. Такое происходит, если каждый раз в качестве центрального элемента выбирается максимум или минимум входной последовательности. Если данные взяты случайно, вероятность этого равна 2/n. И эта вероятность должна реализовываться на каждом шаге... Вообще говоря, малореальная ситуация.

Метод неустойчив. Поведение довольно естественно, если учесть, что при частичной упорядоченности повышаются шансы разделения массива на более равные части.

Сортировка использует дополнительную память, так как приблизительная глубина рекурсии составляет O(log n), а данные о рекурсивных подвызовах каждый раз добавляются в стек.