Отыскание исходного опорного плана ЗЛП методом искусственного базиса
Таблица 3.14
Таблица 3.13
Таблица 3.12
Таблица 3.11
Таблица 3.8
Таблица 3.7
Таблица 3.6
| Б | 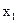
| 
| 
| 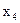
| 
| Q |
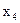
| 
| 
| ||||

| 
| |||||

| ||||||
| f | 
| 
| -2 |
Обратим внимание, что в столбце Q в первых трех строках стоят неотрицательные числа, т.е. новый базис  по-прежнему является допустимым. Это не случайный факт: так будет всегда при точном соблюдении правила выбора генеральной строки. Далее, значение целевой функции при новом опорном плане равно -2, при старом оно было равно 12. "Улучшение" опорного плана гарантирует правило выбора генерального столбца. Хотя эти факты мы строго не доказываем, следует иметь в виду, что они всегда имеют место.
по-прежнему является допустимым. Это не случайный факт: так будет всегда при точном соблюдении правила выбора генеральной строки. Далее, значение целевой функции при новом опорном плане равно -2, при старом оно было равно 12. "Улучшение" опорного плана гарантирует правило выбора генерального столбца. Хотя эти факты мы строго не доказываем, следует иметь в виду, что они всегда имеют место.
Посмотрев на таблицу З.6 , мы видим, что не выполняются ни условие оптимальности опорного плана, ни условие неразрешимости ЗЛП. Значит, надо снова выбирать генеральный элемент и переходить к новой симплекс-таблице. Читатель сможет проделать это самостоятельно.
3.6. Табличный симплекс-алгоритм.
Пусть имеется заполненная симплекс-таблица. Подводя итоги изложенному, получим следующий алгоритм решения ЗЛП симплекс-методом.
1. Если в нижней строке симплекс-таблицы все числа, кроме, быть может, самого правого, неположительны, то опорный план, соответствующий симплекс-таблице, оптимален, и алгоритм останавливается. В противном случае - переход пункту 2.
2. Если симплекс-таблица содержит столбец, отличный от самого правого, у которого в нижней строке стоит положительное число, а во всех остальных строках - неположительные числа, то ЗЛП неразрешима из-за неограниченности снизу на ОДР целевой функции, и алгоритм останавливается. В противном случае - переход к пункту 3.
3. Выбираем любой столбец, отличный от самого правого, у которого в нижней строке стоит положительное число - назовем его генеральным. Затем рассматриваем строки симплекс-таблицы, отличные от самой нижней, у которых в генеральном столбце стоят положительные числа. Для каждой из таких строк вычисляем отношение свободного члена к элементу, стоящему в генеральном столбце. Строка, для которой это отношение минимально, является генеральной строкой. Элемент, стоящий на пересечении генерального столбца и генеральной строки, будет генеральным элементом. Переход к пункту 4.
4. Составляем новую симплекс-таблицу, в которой:
1) из базиса выведена переменная, стоящая в генеральной строке; в базис введена переменная, стоящая в генеральном столбце;
2) генеральная строка поделена на генеральный элемент;
3) с помощью жордановой процедуры все числа генерального столбца, за исключением 1, стоящей в генеральной строке, делаются равными нулю. Переход к пункту 1.
Пример I. Решить симплекс-методом



Задача записана в каноническом виде, нужно привести ее к табличному виду. Система уравнений записана в жордановой форме с неотрицательными правыми частями (базисные переменные  и
и 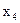 ). Необходимо привести к табличному виду целевую функцию. Для этого выразим базисные переменные через свободные
). Необходимо привести к табличному виду целевую функцию. Для этого выразим базисные переменные через свободные
x3=10 - 2x1 - x2
x4= 8 - x1 - 2x2
и подставим в целевую функцию

Для получения табличного вида функцию запишем так:

Теперь имеем табличный вид ЗЛП:

Заполним первую симплекс-таблицу
| Б | 
| 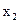
| 
| 
| Q |

| |||||

| |||||
| F |
В таблице 3.7 условия оптимальности и неразрешимости не выполняются. Выберем в качестве генерального столбец 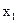 , у которого в нижней строке стоит положительное число. Затем, сравнивая отношения 10:3 и 8:1, выберем первую строку в качестве генеральной. В таблице генеральный элемент 2 .
, у которого в нижней строке стоит положительное число. Затем, сравнивая отношения 10:3 и 8:1, выберем первую строку в качестве генеральной. В таблице генеральный элемент 2 .
Действуя в соответствии с пунктом 4 табличного симплекс-алгоритма, перейдем к таблице 3.8.
| Б | 
| 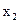
| 
| 
| Q |

| 
| 
| |||

| 
| 
| |||
| F | -5 | -22 |
Условия оптимальности и неразрешимости не выполняются. Выбираем в таблице 3.8 генеральный элемент и переходим к следующей таблице
Таблица 3.9
| Б | 
| 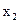
| 
| 
| Q |

| 
| 
| |||
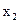
| 
| 
| |||
| F | 
| 
| -24 |
Таблица 3.9 удовлетворяет условию оптимальности.
Ответ: оптимальный план 
Минимальное значение целевой функции fmin = - 24.
Пример 2. Решить симплекс-методом:


Прежде всего, ЗЛП нужно привести к каноническому виду


Теперь приводим ЗЛП к табличному виду. Видим, что система уравнений записана в жордановой форме с неотрицательными правыми частями ( и z- базисные переменные). Однако в целевую функцию входит базисная переменная
и z- базисные переменные). Однако в целевую функцию входит базисная переменная . Имеем:
. Имеем:



Следовательно, табличный вид ЗЛП таков:

Заполняем симплекс-таблицу (таблица 3.10).
Таблица 3.10
| Б | 
| 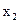
| 
| z | Q |

| -1 | ||||
| z | -2 | ||||
| g | -1 |
После выбора генерального элемента переходим к таблице 3.11
| Б | 
| 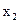
| 
| z | Q |

| -1 | ||||
| z | -2 | ||||
| g | -2 | -9 |
Обратим внимание на столбец
 . Он показывает, что целевая функция g не ограничена снизу на ОДР. Вспоминая, что g =-f, получаем ответ.
. Он показывает, что целевая функция g не ограничена снизу на ОДР. Вспоминая, что g =-f, получаем ответ.
Ответ: ЗЛП неразрешима из-за неограниченности сверху на ОДР целевой функции f.
Пример 3. Решим симплекс-методом задачу об использовании оборудования, поставленную в параграфе 2.1. Там же приводилась ее математическая модель


Приводим ЗЛП к каноническому виду




Система уравнений записана в жордановой форме с неотрицательными правыми частями, базисные переменные  не входят в целевую функцию g. Поэтому табличный вид целевой функции таков:
не входят в целевую функцию g. Поэтому табличный вид целевой функции таков: .
.
Заполняем симплекс-таблицу (таблица 3.12).
| Б | 
| 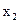
| 
| 
| 
| Q |

| ||||||

| ||||||

| ||||||
| G |
Условия оптимальности и неразрешимости не выполняются. Столбец  (в нижней строке которого стоит наибольшее положительное число) выберем в качестве генерального. Сравнивая отношения 30:3, 40:2, и 60:4, объявляем генеральной первую строку. Поделив ее на 3 и сделав с помощью жордановой процедуры нули во всех остальных строках генерального столбца, после замены базисной переменной
(в нижней строке которого стоит наибольшее положительное число) выберем в качестве генерального. Сравнивая отношения 30:3, 40:2, и 60:4, объявляем генеральной первую строку. Поделив ее на 3 и сделав с помощью жордановой процедуры нули во всех остальных строках генерального столбца, после замены базисной переменной  на переменную
на переменную 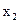 , получим таблицу 3.13.
, получим таблицу 3.13.
| Б | 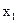
| 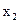
| 
| 
| 
| Q |
| x2 | 
| 
| ||||
| z2 | 
| 
| ||||

| 
| 
| ||||
| g | 
| 
| -70 |
Снова выбираем генеральный элемент и переходим к таблице 3.14
| Б | 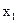
| 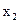
| 
| 
| 
| Q |
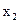
| 
| 
| ||||
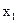
| 
| 
| 
| |||

| 
|  
| 
| |||
| g | - 2 | 
| -80 |
В нижней строке таблицы 3.14 стоят неположительные числа. Поэтому опорный план, соответствующий этой таблице, оптимален. Выпишем его:

Так как переменные  не фигурировали в исходной постановке задачи, кроме того, функция f = - g в исходной постановке максимизировалась, то можно записать следующее оптимальное решение исходной задачи
не фигурировали в исходной постановке задачи, кроме того, функция f = - g в исходной постановке максимизировалась, то можно записать следующее оптимальное решение исходной задачи

Возвращаясь к содержательной постановке (параграф 2.1), получаем следующий вывод: прибыль предприятия будет максимальной (равной 80 ден.ед.), если изделий А выпустить 7,5 ед., изделий В выпустить 5 ед.
Эту же задачу мы решили геометрически (см. параграф 2.5, пример 5) и, естественно, получили тот же результат.
Чтобы начать решение ЗЛП симплекс-методом, нужно привести ее сначала к каноническому виду, а потом - к табличному. Табличный вид требует, чтобы система уравнений канонического вида была приведена к жордановой форме с неотрицательными правыми частями. Базисное решение такой жордановой формы будет исходным опорным планом ЗЛП.
Приведение системы линейных уравнений к жордановой форме не представляет труда, однако требование неотрицательности правых частей усложняет задачу. Кроме того, если ОДР задачи пуста, то жордановой формы с неотрицательными правыми частями не существует (хотя жорданову форму система линейных уравнений может иметь).
Систематическая процедура, которая либо обнаруживает неразрешимость ЗЛП из-за пустоты ОДР, либо приводит систему линейных уравнений канонического вида к жордановой форме с неотрицательными правыми частями (отыскивает исходный опорный план) называется методом искусственного базиса. Приступим к изложению этого метода.
Пусть ЗЛП записана в каноническом виде.
 (3.5)
(3.5)

Прежде всего нужно сделать неотрицательными правые части системы (3.6). Этого можно добиться умножением на (-1) уравнений с отрицательными правыми частями. Итак, будем считать, что
 (3.8)
(3.8)
Рассмотрим вспомогательную задачу, которая записывается следующим образом:
 (3.9)
(3.9)

Переменные  называются искусственными. Они образуют базис в жордановой форме (3.10), который называется искусственным базисом.
называются искусственными. Они образуют базис в жордановой форме (3.10), который называется искусственным базисом.
ОДР вспомогательной задачи непуста, так как ей принадлежит следующий набор значений переменных:  (см.(3.10),(3.11),(3.12)(3.8)). Целевая функция (3.9), являющаяся суммой неотрицательных переменных, ограничена снизу на ОДР нулем:
(см.(3.10),(3.11),(3.12)(3.8)). Целевая функция (3.9), являющаяся суммой неотрицательных переменных, ограничена снизу на ОДР нулем: . Таким образом, для вспомогательной задачи ни одна из двух причин неразрешимости не имеет места, и, следовательно,вспомогательная задача разрешима. Так как система уравнений записана в жордановой форме с неотрицательными правыми частями, то мы можем привести вспомогательную задачу к табличному виду и решить симплекс-методом. После решения могут представиться два случая.
. Таким образом, для вспомогательной задачи ни одна из двух причин неразрешимости не имеет места, и, следовательно,вспомогательная задача разрешима. Так как система уравнений записана в жордановой форме с неотрицательными правыми частями, то мы можем привести вспомогательную задачу к табличному виду и решить симплекс-методом. После решения могут представиться два случая.
1.  (3.I3)
(3.I3)
Покажем, что тогда исходная задача (3.5 - 3.7) неразрешима из-за пустоты ОДР. Действительно, пусть, вопреки этому утверждению, есть допустимое решение  исходной задачи. Тогда набор значений переменных
исходной задачи. Тогда набор значений переменных

является, очевидно, допустимым решением вспомогательной задачи. Значение целевой функции F при этом допустимом решении равно 0, что противоречит (3.13).
2.  (3.14)
(3.14)
Рассмотрим последнюю симплекс-таблицу для вспомогательной задачи. Выпишем соответствующую этой таблице жорданову форму с неотрицательными правыми частями. Здесь могут представиться две возможности:
а) среди базисных переменных нет искусственных. Тогда удалим из жордановой формы все члены, содержащие искусственные свободные переменные, получим жорданову форму с неотрицательными правыми частями для исходной задачи;
б) среди базисных переменных есть искусственные. Учитывая (3.9) и (3.14), можно утверждать, что в оптимальном плане значения всех искусственных переменных равны 0. Поэтому правая часть каждого уравнения, содержащего искусственную переменную в качестве базисной, равна 0, т.е. такое уравнение можно записать так:
 (3.15)
(3.15)
Далее, если в уравнении (3.15) коэффициенты при всех переменных  равны 0 (иначе говоря, оно фактически содержит только искусственные переменные), то удалим такое уравнение из жордановой формы. Если же уравнение вида (3.15) содержит какую-либо переменную
равны 0 (иначе говоря, оно фактически содержит только искусственные переменные), то удалим такое уравнение из жордановой формы. Если же уравнение вида (3.15) содержит какую-либо переменную  с ненулевым коэффициентом, то поделим уравнение на коэффициент при
с ненулевым коэффициентом, то поделим уравнение на коэффициент при  , получим уравнение вида:
, получим уравнение вида:
 (3.16)
(3.16)
С помощью жордановой процедуры исключим  из остальных уравнений системы. Так как правая часть уравнения (3.16) равна 0, то правые части остальных уравнений после исключения
из остальных уравнений системы. Так как правая часть уравнения (3.16) равна 0, то правые части остальных уравнений после исключения  не изменятся и останутся неотрицательными.
не изменятся и останутся неотрицательными.
С помощью указанных приемов мы всегда можем получить жорданову форму с неотрицательными правыми частями, среди базисных переменных которой нет искусственных, и прийти, таким образом, к случаю а).
Пример I. Решить симплекс-методом


Задача записана в каноническом виде, однако правая часть второго уравнения системы отрицательна. Поэтому систему уравнений перепишем так:

Запишем вспомогательную задачу


Решим вспомогательную задачу симплекс-методом. Для этого приведем ее к табличному виду

Табличный вид вспомогательной задачи таков:

Построим первую симплекс-таблицу (таблица 3.15)