Основы математической обработки геодезических измерений

Геодезические измерения определяют относительное положение точек земной поверхности.

Различают следующие виды измерений:

1) линейные – получают наклонные и горизонтальные расстояния между точками. Инструменты: мерные ленты, рулетки, проволоки, оптические свето- и радиодальномеры;

2) угловые – определяют величины горизонтальных и вертикальных углов. Инструменты: эклиметры, буссоли, теодолиты;

3) высотные – получают разности высот отдельных точек. Инструменты: баронивелиры, теодолиты-тахеометры, нивелиры.

Измерения бывают:

1) непосредственные (прямые);

2) косвенные.

Измерения бывают:

1) равноточные (один объект наблюдения, один наблюдатель, один мерный прибор, одна методика наблюдений, одинаковые условия внешней среды);

2) неравноточные (когда не соблюдаются выше перечисленные условия).

Измерения сопровождаются погрешностями (ошибками): грубыми (из-за невнимательности наблюдателя), систематическими (из-за несовершенства приборов) и случайными (зависящими от многих причин и неподдающимися никаким прогнозам).

Грубые погрешности исключают повторными наблюдениями. Систематические погрешности можно учесть, вводя поправки в измеренные величины за длину ленты, длину метра реек, за погрешности прибора и т.д. Случайные погрешности исключить нельзя, но можно ослабить их влияние на измеренные величины путем многократных наблюдений.

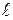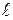Имеем ряд измерений ₁, ₂ ….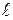_n одной и той же величины, истинное значение которой Х. Случайные погрешности этих измерений D_i = 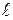_i - Х. Ряд случайных погрешностей D₁, D₂ …. D_n имеет свойства:

1) свойство ограниченности – все случайные погрешности должны быть меньше заранее известного предела

D £ D_пред;

2) свойство симметричности – число положительных и отрицательных погрешностей должно быть одинаковым

– D » + D;

3) свойство унимодальности – малые по абсолютной величине погрешности должны встречаться чаще, чем большие

D > D;

 

4) свойство компенсации – при неограниченном числе измерений предел среднего значения погрешностей стремится к нулю

.

 

 

Если Х неизвестно Имеем ряд измерений 1, 2 ….n.

Если Х известно Имеем ряд измерений 1, 2 ….n. Ряд истинных погрешностей D1 = 1 – Х, D2 = 2 – Х, ………….. Dn = n – Х. Сложим члены уравнений

		Ряд вероятнейших погрешностей
		Сложим члены уравнений
		Формула Бесселя
	Формула Гаусса

 

Виды погрешностей:

- случайная (абсолютная) погрешность D = 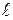– Х;

- вероятнейшая погрешность v;

- средняя квадратическая погрешность m;

- относительная погрешность ;

- предельная погрешность D_пред = 2m.