Прямая и обратная геодезические задачи. Их применение в геодезическом производстве

Рис. 3.5. Прямая геодезическая задача

Дано: координаты точки 1 х₁, у₁; горизонтальное проложение линии 1 – 2: d_1,2;

дирекционный угол линии 1 – 2: a_1,2 (рис.3.5).

Найти: координаты точки 2: х₂, у₂.

Решение: координаты точки 2: х₂ = х₁ + Dх; у₂ = у₁ + Dу, (3.6)

где приращения координат Dх = d · cos a; Dу = d · sin a, (3.7)

откуда х₂ = х₁ + d · cos a; у₂ = у₁ + d · sin a. (3.8)

Знаки приращений координат Dх и Dу зависят от знаков функций sin a и cos a.

б) Обратная геодезическая задача

Рис. 3.6. Обратная геодезическая задача

Дано: координаты точек 1 и 2: х₁, у₁; х₂, у₂ (рис.3.6).

Найти: горизонтальное проложение линии 1 – 2: d_1,2; дирекционный угол линии 1 – 2: a_1,2.

Решение: Dх = х₂ – х₁; Dу = у₂ – у₁; (3.9)

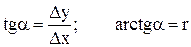; (3.10)

. (3.11)

По значению tg a определяется румб линии. По знакам приращений координат определяется четверть, а по четверти определяется дирекционный угол линии.

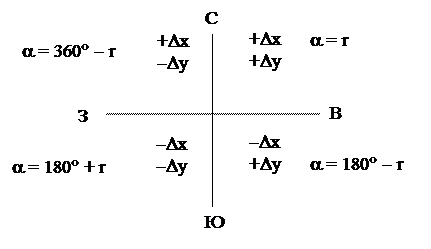
Рис. 3.7. Знаки приращений координат

в зависимости от четверти

Прямая геодезическая задача применяется при вычислении координат в теодолитном ходе. Обратная геодезическая задача применяется в тех случаях, когда по известным координатам 2-х точек определяют расстояние между ними и дирекционный угол линии.