Ориентирование линий в геодезии
Тема 3. Ориентирование
Ориентирование линий в геодезии. Дирекционный угол, истинный и магнитный азимуты, румбы. Сближение меридианов и магнитные склонения, их использование при вычислении азимутов. Прямая и обратная геодезические задачи. Применение их в геодезическом производстве.
Ориентировать – значит найти направление заданной линии относительно другого направления, принятого за исходное.
За исходное направление в геодезии принимают:
а) Астрономический (истинный меридиан)
 |
Рис. 3.1. Истинный азимут
А – астрономический (истинный) азимут линии – горизонтальный угол, отсчитываемый в данной точке от северного конца истинного меридиана по ходу часовой стрелки до направления ориентируемой линии (рис.3.1).
А – прямой истинный азимут, Аобр – обратный.
б) Магнитный меридиан

Рис. 3.2. Магнитный азимут
Ам – магнитный азимут линии – горизонтальный угол, отсчитываемый в данной точке от северного конца магнитного меридиана по ходу часовой стрелки до направления ориентируемой линии (рис.3.2),
А – истинный азимут,
d – склонение магнитной стрелки – угол между истинным и магнитным меридианами.
d со знаком «+» при положении магнитного меридиана вправо от истинного меридиана, и со знаком «–» при положении влево.
Ам = А – d (3.1)
Пример 1:
Ам = 308°33¢, d = - 6° 27¢. Найти А.
А = Ам + d = 308°33¢ - 6° 27¢ = 302°06¢.
 |
 в) Осевой меридиан зоны
в) Осевой меридиан зоны
Рис. 3.3. Дирекционный угол
a – дирекционный угол линии – горизонтальный угол, отсчитываемый в данной точке от северного конца осевого меридиана или линии, ему параллельной, по ходу часовой стрелки до направления ориентируемой линии (рис.3.3).
a – дирекционный угол линии LN, aобр – дирекционный угол линии NL.
Связь прямого и обратного дирекционных углов можно выразить уравнением:
aобр = a ± 180°. (3.2)
Связь истинного азимута и дирекционного угла выражается формулой
А = a + g, (3.3)
где g – сближение меридианов – угол между истинным и осевым меридианами.
g имеет знак «+», если осевой меридиан расположен вправо от истинного меридиана, и знак «–»,если осевой меридиан расположен влево от истинного меридиана.
Пример 2: g = -2° 35¢, a = 168° 47¢. Вычислить А.
 А = a + g = 168° 47¢ + (-2° 35¢) = 166° 12¢.
А = a + g = 168° 47¢ + (-2° 35¢) = 166° 12¢.
Пример 3: g = + 4° 11¢, А = 312° 56¢. Вычислить a.
 А = a + g; a = А -g = 312° 56¢ - 4° 11¢ = 308° 45¢.
А = a + g; a = А -g = 312° 56¢ - 4° 11¢ = 308° 45¢.
г) Румбы
Иногда вместо дирекционных углов используют румбы. Румб – острый угол, отсчитываемый от ближайшего (северного или южного) конца осевого меридиана до направления определяемой линии (рис.3.4).
Связь между дирекционными углами и румбами:
СВ: r = a;
|
ЮЗ: r = a - 180°, a = 180° + r;
СЗ: r = 360° - a, a = 360° - r.
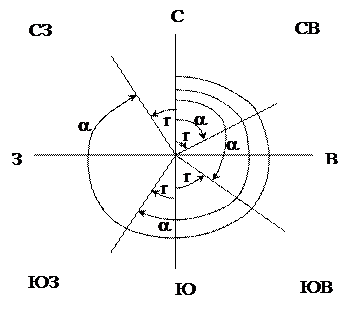 |
 Рис. 3.4. Румбы
Рис. 3.4. Румбы
|
Ам = А – d; (3.5)
Ам = a + g – d.
Пример 4:
r = ЮЗ: 56°41¢, a = 180° + 56°41¢ = 236°41¢.
 |
Пример 5:
a = 92°11¢, g = - 4° 30¢, d = - 9° 42¢. Найти А и Ам.
А = 92°11¢ - 4° 30¢ = 87°41¢,
Ам = 87°41¢ + 9° 42¢ = 97°23¢.
 |