Примеры решения задач

Задача 119. Дисперсия каждой из попарно независимых случайных величин не превышает 10. Требуется:

а) Оценить вероятность того, что модуль отклонения средней арифметической шестнадцати тысяч этих величин от ее математического ожидания не превышает 0,25. б) Определить, сколько таких случайных величин нужно взять, чтобы с вероятностью, не меньшей 0,995, можно было утверждать, что абсолютная величина разности - -M() не превысит 0,25.

Решение. Так как дисперсия суммы попарно независимых случайных величин равна сумме дисперсий слагаемых, то

=, так как для всех i. Тогда

Чтобы ответить на второй вопрос, нужно определить число случайных величин из условия

откуда n ³32000.

Задача 120. Оценить вероятность того, что при 3600 независимых бросаниях кубика число появлений 6 очков будет не меньше 900.

Решение. Случайная величина X – число появлений 6 очков в 3600 бросаниях кубика – имеет математическое ожидание

Тогда по неравенству Чебышева при e = 900 имеем

Вычислим ту же вероятность, используя интегральную теорему Лапласа.

p = 1/6; q = 5/6; np = 3600·1/6 = 600; npq = 600·5/6 = 500;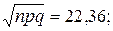

k₁= 900; k₂= 3600; ; (134,16) = 0,5;

(13,42) = 0,5. Так что искомая вероятность практически равна 0. Неравенство Чебышева дало очень грубую оценку.

Задача 121. Устройство состоит из 10 независимо работающих элементов. Вероятность отказа каждого элемента равна 0,05. Оценить вероятность того, что модуль разности между числом отказавших элементов и средним числом отказов окажется не меньше двух.

Решение. Пусть X – число отказавших элементов. Тогда ε = 2; n = 10;

p = 0,05; q = 0,95; M(X)= np = 0,5; D(X)= npq = 0,475.

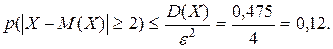
Пользоваться нормальным законом распределения в этом случае нельзя, так как вероятность p мала, кроме того, 3σ(X)= 2,07; np - 3σ(X)= 0,5 - 2,07= -1,57 < 0.

Если бы мы подсчитывали число работающих элементов, то вероятность p равнялась бы 0,95, и тогда .

Задача 122. Оценить вероятность того, что частота появления шестерки в 10000 независимых бросаниях кубика отклонится от вероятности появления шестерки по абсолютной величине меньше чем на 0,01.

Решение. Если Х – число появлений шестерки в n независимых бросаниях кубика, то частота появления шестерки – это случайная величина 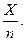Отсюда, если ,

В соответствии с центральной предельной теоремой мы можем считать, что случайная величина 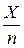имеет приближенно нормальное распределение с математическим ожиданием, равным , и дисперсией, равной Тогда

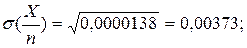
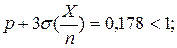
Задача 123. Вероятность появления события А в каждом испытании равна 0,5. Оценить вероятность того, что в 100 независимых испытаниях событие А появится от 40 до 60 раз.

Решение. Случайная величина Х – число появления события А в 100 независимых испытаниях – имеет биноминальное распределение с математическим ожиданием М(Х) = 100·1/2 = 50 и дисперсией Значит, нужно оценить вероятность события Следовательно,

Использование нормального закона дает такой результат:

Число опытов n невелико, поэтому снова получается большое расхождение с оценкой по неравенству Чебышева.

Между тем 35 > 0; 65 < 100, поэтому применение центральной предельной теоремы правомерно.

При решении следующих задач подразумевается возможность использования нормального распределения.

Задача 124. Монета брошена 2N раз (N велико). Найти вероятность того, что герб выпадает ровно N раз.

Решение. n = 2N, k = N, p = q = 0,5; Так как j(0) = = 0,3989, имеем

Задача 125. Вероятность появления некоторого события A в каждом из 2100 независимых испытаний равна 0,7. Найти вероятность того, что это событие появится: а) не менее 1470 и не более 1500 раз; б) не менее 1470 раз; в) не более 1469 раз.

Решение. Воспользуемся интегральной теоремой Муавра - Лапласа.

а) По условию Тогда ; , .

По таблице значений функции Лапласа определяем, что = 0, 1,43) = 0,4236. Тогда искомая вероятность равна

б) Событие A должно появиться не менее 1470 раз, но оно не может появиться более 2100 раз, поэтому х₁ = 0, . Так как для всех значений аргумента x функции Лапласа, больших пяти, можно считать, что = 0,5, получаем, что .

в) События {событие А появилось не менее 1470 раз} и {событие А появилось не более 1469 раз} противоположны, поэтому

Задача 126. Вероятность появления положительного результата в каждом из n опытов равна 0,8. Сколько нужно произвести опытов, чтобы с вероятностью 0,9 можно было ожидать, что не менее 75 опытов дадут положительный результат?

Решение. По условию

Нужно найти n. Таким образом,

где . Очевидно, что n > 75, поэтому .

Можно положить, что тогда то есть По таблице функции Лапласа находим, что аргумент, для которого функция Лапласа равна 0,4, равен 1,26. Функция Лапласа нечетна, поэтому . Окончательно Если обозначить через х, получается квадратное уравнение откуда

Так как отрицательный корень не подходит, остается одно значение = 10; n = 100.