Отображение или зеркалирование

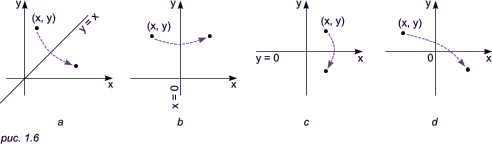
• Зеркалирование относительно прямой y = x (рис. 1.6a):
  
• Зеркалирование относительно прямой x = 0 (рис. 1.6b):
  
• Зеркалирование относительно прямой y = 0 (рис. 1.6c):
  
• Зеркалирование относительно начала координат (рис. 1.6d):
  

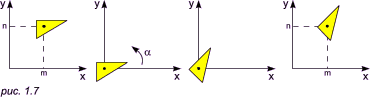
Поворот фигуры вокруг произвольной точки (m, n) на произвольный угол α

Чтобы провести любое сложное преобразование, необходимо разложить его на базовые операции. Поворот фигуры вокруг произвольной точки (m, n) на произвольный угол α состоит из трех базовых операций: 1) перенос фигуры на вектор A(-m, -n) для совмещения точки (m, n) с началом координат; 2) поворот фигуры на угол α; 3) перенос фигуры на вектор A'(m, n) для возвращения ее в исходное положение. Так как фигуру можно представить набором точек, то операции 1) - 3) можно выполнять последовательно для каждой точки. Покажем это на примере.

Пусть мы хотим повернуть треугольник с координатами A(x, y), B(x₁, y₁), C(x₂, y₂) вокруг точки D(m, n) на угол α. Пусть P_-s — матрица переноса точки на вектор A(-m, -n), V_a — матрица поворота на угол a, P_s — матрица переноса точки на вектор A'(m, n).

Итак, мы имеем все данные, необходимые для проведения сложного преобразования первой точки A(x, y):

Точно такие же преобразования необходимо провести для оставшихся двух точек треугольника, подставляя соответствующие их координаты взамен x и y (последовательность операций см. на рис. 1.7). Таким образом, сложная операция разбивается на простейшие и задается произведением соответствующих матриц преобразования, причем порядок, в котором перемножаются матрицы, существенно определяет результат.

Центральное проецирование (перспектива)

px + qy + 1 = H — плоскость.