Вычисление моментов инерции и моментов сопротивления для простейших сечений.

ИЗГИБ.

Известно, что интеграл вида 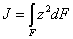является моментом инерции сечения относительно нейтральной оси (ось, проходящая через центр тяжести сечения: сечение, подвешенное за эту точку, при повороте остается неподвижным).

Здесь — расстояние элементарной площадки dF от нейтральной оси; суммирование охватывает всю площадь сечения.

1. Покажем в качестве примера вычисление этого интеграла для прямоугольника (Рис.16) высотой h и шириной b. Проведем через его центр тяжести О оси симметрии Oz и Оу. Если внешние силы, действующие на балку, лежат в плоскости Oz, то нейтральной осью будет ось Оу. Найдем относительно этой оси сначала момент инерции, а потом и момент сопротивления площади прямоугольника.

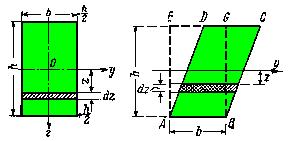
Рис.16. Расчетная модель для определения осевого момента инерции прямоугольника.

Площадки dF, на которые следует разбить всю площадь сечения, выберем в виде узких прямоугольников шириной b и высотой dz (Рис.16.а). Тогда:

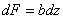
и интеграл J принимает вид:

Чтобы взять интеграл по всей площади прямоугольника, следует z менять от до 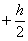. Тогда

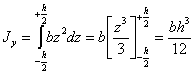Момент сопротивления относительно нейтральной оси Оу мы получим, разделив J_y на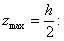

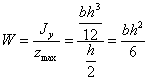
Если необходимо вычислить момент инерции и момент сопротивления прямоугольника относительно оси Oz, то в полученных формулах следовало бы b и h поменять местами: и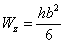

Заметим, что сумма произведений 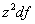не изменится, если мы сдвинем все полоски Df = bdz параллельно самим себе так, что они расположатся в пределах параллелограмма ABCD.

Иначе, момент инерции параллелограмма относительно оси у равен моменту инерции равновеликого ему прямоугольника

2. При вычислении момента инерции круга радиуса 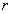(Рис.17) также разбиваем площадь на узкие полоски размером 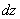вдоль оси Oz; ширина этих полосок b = b(z) тоже будет переменной по высоте сечения. Элементарная площадка

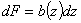
Момент инерции равен:

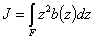
Рис.17. Расчетная модель для определения осевого момента инерции кругового сечения.

Так как верхняя и нижняя половины сечения одинаковы, то вычисление момента инерции достаточно провести для одной нижней и результат удвоить. Пределами для изменения z будут 0 и :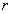

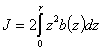
Введем новую переменную интегрирования — угол 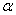(Рис.2); тогда

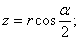
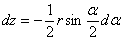
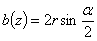
Пределы: при ; при , следовательно,