Тема 3. Дробление и измельчение.

Конструкции классификаторов. Гравитационные и центробежные классификаторы, воздушные сепараторы

Процесс классификации

Классификация процессов разделения по крупности

 

Классификацией называется процесс разделения материа­ла на классы крупности по скоростям падения зерен в жидкой или газообразной среде под действием силы тяжести (в грави­тационном поле), центробежной силы (в центробежном поле) или при одновременном действии этих сил. При этом, если классификация осуществляется в водной среде, она называется гидравлической, если в воздушной среде — пневматической. Гидравлическую классификацию производят в классифи­каторах и гидроциклонах, пневматическую — в воздушных сепараторах. При разделении на два класса крупный продукт называют песками, а мелкий сливом (при гидравлической классификации) или тонким продуктом (при пневматической классификации).

Классифика­ция делит материал по равнопадаемости, т. е. каждый класс, полученный при классификации, содержит крупные зерна лег­ких минералов и мелкие зерна тяжелых минералов, имеющие одинаковые скорости падения в среде.

 

2.2.1. Закономерности свободного и стеснённого падения частиц в водной и воздушной средах.

 

Классификация происходит в условиях свободного или стесненного падения зерен. Свободное падение представляет собой движение единичных зерен в среде, исключающей их взаимное воздействие друг на друга. Под стесненным падени­ем понимается движение множества зерен в виде такой массы, когда помимо гравитационных сил и сил сопротивления сре­ды на движение зерен оказывает влияние динамическое воз­действие непрерывно сталкивающихся окружающих зерен.

Скорость свободного падения зерна определяется соотно­шением силы тяжести, подъемной (архимедовой) силы и силы со­противления среды, которая зависит от режима движения зерна.

При ламинарном режиме тело движется с малой скоро­стью, потоки среды как бы омывают его, не образуя завихре­ний. Сопротивление Р_В определяется главным образом вязко­стью среды μ и количественно описывается законом Стокса:

(2.5)

где v - скорость движения зерна; d - диаметр зерна.

Турбулентный режим движения характерен для высоких скоростей движения и сопровождается образованием вихрей у поверхности тела и позади него. Динамическое или инерци­онное сопротивление среды перемещению тела изменяется в этом случае по закону Ньютона — Риттингера:

(2.6)

где k — коэффициент (равный 1/2, по Риттингеру); F - площадь проекции тела (равнадля шара);— плотность среды.

В реальных условиях движущееся зерно испытывает од­новременное действие как сопротивления от вязкости Р_в, так и динамического сопротивления Р_д, но степень их проявления различна. Характеристикой соотношения сил сопротивлений Р_д и Р_в и, следовательно, режима движения минерального зер­на в среде является безразмерный параметр Рейнолъдса (Rе)

откуда в общем виде:

(2.7)

При значениях Rе < 1 наблюдается ламинарный режим движения частиц, размер которых не превышает 0,1 мм. При значениях Rе > 1000 и размере частиц более 2 мм наблюдается турбулентный режим движения. Переходной области от лами­нарного к турбулентному режиму движения отвечают значе­ния Rе от 1 до 1000, а крупность частиц от 0,1 до 2 мм. Сопротивление среды для этой области можно рассчитать по формуле Аллена:

(3.8)

Если подставить значение ц из формулы (3.7) в выраже­ние (2.5) (2.9)

и сравнить выражения для Р_д [формула (3.6)], для Р_а[формула (2.8)] и для Р_в [формула (2.9)], то обнаружим, что общий закон сопротивления среды движению зерна описывается формулой

P = Ψv²d²Δ (2.10)

где Ψ=.f(Re) — коэффициент сопротивления. Графическое изо­бражение зависимости Ψ=.f(Re) в логарифмических коорди­натах, носящее название диаграммы Рейлея (рис. 2.5, кривая Ψ), указывает на постепенный переход от ламинарного к турбу­лентному режиму движения по мере возрастания параметра Rе.

Рис. 2.5.Зависимость коэффициента сопротивления Ψ и параметра Re²Ψ от числа Рейнольдса (Rе)

 

Гравитационная сила G, вызывающая падение зерна, бу­дет определяться весом тела в среде. В соответствии с законом Архимеда для шарообразного тела объемом

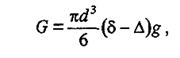(2.11)

где δ — плотность зерна; g — ускорение силы тяжести.

Результирующая сила Р₁ускоряющая движение зерна в среде, определится как разность между гравитационной силой G и силой сопротивления Р [формула (2.10)]

или (2.12)

Увеличение скорости движения частиц в начальный мо­мент под действием гравитационной силы вызывает возрас­тающее сопротивление среды и через доли секунды частица начинает падать с постоянной скоростью v₀

В этих условияхи

откуда (для общего случая):

(2.13)

При ламинарном режиме, на основании уравнений (2.5) и (2.11):

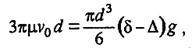
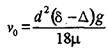(закон Стокса). (2.14)

При переходном режиме, на основании формул (2.8) и (2.11):

С учетом выражения для Rе:

(закон Алена) (2.15)

При турбулентном режиме, на основании формул (2.6) и (2.11):

(закон Риттингера). (2.16)

Универсальный метод, пригодный для определения ко­нечных скоростей движения зерен любой крупности, плотно­сти, формы, предложил П.В. Лященко. Он учел, что на основа­нии формул (2.7) и (2.10) можно составить систему уравнений:

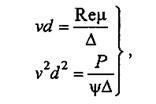(2.17)

в результате совместного решения которой получим выраже­ние для параметра Rе² Ψ

(2.18)

Поскольку при установившемся движении Р = G, то, под­ставляя в формулу (2.18) вместо Р выражение для G из фор­мулы (2.11), находим:

(2.19)

По уравнению (2.19) на основании известных параметров зерна и среды легко рассчитать значение параметра Rе²Ψ и ис­пользовать его для определения параметра Rе по диаграмме Rе²Ψ = f(Rе), построенной на основе диаграммы Рейлея Ψ =f(Re) и изображенной на рис. 2.5. После этого можно опре­делить конечную скорость падения частицы или непосредст­венной подстановкой полученного значения Rе в формулу (2.7) или подстановкой значения Ψ, найденного по значению Rе на диаграмме Рейлея (см. рис. 2.5, кривая Ψ), в формулу (2.13).

Пример 1. Определить конечную скорость движения в воде зерна угля размером d = 25 мм (0,025 м), плотностью δ = 1350 кг/м³, принимая дина­мический коэффициент вязкости воды при температуре 293 К равным μ = 0,001 Н-с/м², плотность Δ = 1000 кг/м³ g= 9,81 м/с².

По формуле (3.19) значение Rе²Ψ равняется 2807×10⁴. На диаграмме Rе²Ψ = f(Rе) (см. рис. 3.5) этому значению соответствует значение Rе = 12400. По формуле (3.7) v=v₀= 0,496 м/с. Расчет скорости по формуле (3.13) для значения Ψ= 0,183 (соответствующего найденному значению Rе= 12400) показывает идентичные результаты.

Пример 2. Определить конечную скорость движения в воздухе зерна кварца размером d = 1 мм (0,001 м), плотностью δ = 2500 кг/м³, принимая динамический коэффициент вязкости воздуха μ = 0,00002 Н-с/м², плот­ность Δ = 1,23 кг/м³.

По формуле (3.19) значение Rе²Ψ = 39 447. На диаграмме (см. рис. 3.5) этому значению соответствует Rе = 400. По формуле (3.7) скорость v=v₀= 7, 18 м/с.

При расчете скоростей падения зерен неправильной фор­мы пользуются эквивалентным диаметром d_э частиц, т. е. ди­аметром шара, одинакового с частицей объема:

и в расчетные формулы вводят поправочный коэффициент фор­мы К_ф, представляющий собой отношение поверхности равно­великого шара к поверхности зерна неправильной формы и рав­ный: 1,0 — при шарообразной; 0,8—0,9 — -при округлой; 0,7 — 0,8 — при угловатой; 0,6 — 0,7 — при пластинчатой форме частиц.

Скорость стесненного падения v_ст зерен всегда меньше ско­рости их свободного падения v_о (например, для кварца в 2,76 раза, для галенита в 3,47 раза). Установлена существенная за­висимость скорости стесненного падения от степени разрых­ления или взвешенности минеральных частиц в среде, харак­теризуемой коэффициентом разрыхления Θ_Р, равным отно­шению объема свободного пространства между зернами к пол­ному объему, занимаемому разрыхленной смесью (значение всегда меньше 1). По П. В. Лященко,

(2.20)

Формула (2.20) пригодна для определения скорости стес­ненного падения зерен крупностью менее 0,2 мм при класси­фикации тонкозернистого материала. Для определения у_ст бо­лее крупных зерен — от 0,2 до 12,5 мм — пользуются фор­мулой Ханкока:

(2.21)

Зерна различной крупности и плотности, но имеющие оди­наковые конечные скорости движения в среде, называются равнопадающими, т. е. v₀₁=v₀₂. В общем случае на основании формулы 2.13:

Откуда

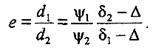(2.22)

Отношение диаметров равнопадающих легкого и тяжело­го зерен называется коэффициентом равнопадаемости (е).

Обозначив через К₁и К₂постоянные коэффициенты, учи­тывающие влияние реологических параметров среды и формы соответственно для легких и тяжелых зерен на основании фор­мул (2.14) — (2.16) находим:

для ламинарного режима движения [формула (2.14)]

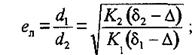(2.23)

для переходного режима движения [формула (2.15)]

; (2.24)

для турбулентного режима движения [формула (2.16]

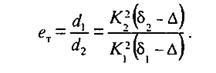(2.25)

В материале, поступающем на гравитационное обогаще­ние, основанное на использовании различия скоростей паде­ния разделяемых зерен, не должны присутствовать их равнопадающие зерна. Для этого материал подвергают предвари­тельной классификации по крупности, шкала (модуль) кото­рой не должна превышать коэффициент равнопадаемости.

 

В зависимости от конструкции классификатора процесс классификации может осуществляться в горизонтальном или восходящем потоке среды под действием гравитационных сил и сил сопротивления, а также в центробежном поле, где клас­сифицируемые частицы испытывают дополнительное воздей­ствие центробежных сил инерции.

При классификации в восходящем потоке (рис. 2.6, а) круп­ность зерен, выделяемых в слив (или пески), определяется со­отношением скорости их падения v₀ и скорости восходящего потока и.

Рис. 2.6. Схема процесса классификации в восходящих (а) и горизонталь­ных (б) потоках

Если для данного зерна v₀ > и, то зерно перейдет в в пески, а если v₀ < и, то зерно будет вынесено потоком в слив классификатора. При получении нескольких классов их выде­ление осуществляется при различных скоростях восходящих по­токов. Отношение значений скоростей восходящих потоков, при которых происходит выделение смежных классов, называ­ется коэффициентом шкалы гравитационной классификации S_Г:

(2.26)

При классификации в горизонтальном потоке (рис. 2.6, б) каждая частица перемещается в горизонтальном направлении со скоростью горизонтального потока среды и и по вертикали под действием силы тяжести с конечной скоростью падения v₀. При глубине сливающегося потока h и длине классификатора l частица уйдет со сливом, если 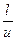< , или в пески, если 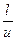> . В граничных условиях 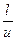= ; v₀= и. Учитывая, что при ширине классификатора b и объеме его слива V:, получаем:

(2.7)

т. е. при классификации в горизонтальном потоке скорость падения и, следовательно, крупность частиц, уходящих со сли­вом, не зависят от глубины потока, а определяются объемом слива V и площадью зеркала классификатора lb, Чем больше объем слива и меньше площадь зеркала классификатора, тем больше конечная скорость падения и крупность частиц, пере­ходящих в слив.

Для классификации в центробежном поле используются или неподвижные цилиндрические аппараты, пульпа или аэросуспензия в которые подается под давлением (0,5—3,0)×10⁵Па тангенциально к внутренней поверхности цилиндра, или вра­щающиеся обычно цилиндрические аппараты. Вращение пуль­пы и образование центробежных полей с ускорением в десят­ки и тысячи g позволяет резко снизить крупность разделения, по сравнению с гравитационной классификацией. Отношение ускорений центробежного а_ци гравитационного а_гсиловых полей называют фактором разделения F_разд

(2.28)

Его значение зависит от числа оборотов п, об/мин, и ра­диуса вращения R, м. Например, при F_разд - 100 частица круп­ностью 30 мкм будет двигаться в центробежном поле с той же скоростью, что и частица размером в 300 мкм в гравитацион­ном поле.

На практике четкость разделения при классификации на­рушается циркуляционным движением потока, перемешивани­ем частиц его турбулентными вихрями и другими причинами технологического характера. Поэтому в песках всегда присут­ствуют мелкие частицы, а в сливе — часть крупных. Оценку ре­зультатов и качества продуктов классификации, а также круп­ности разделения при классификации производят по резуль­татам ситового анализа слива и песков (рис. 2.7).

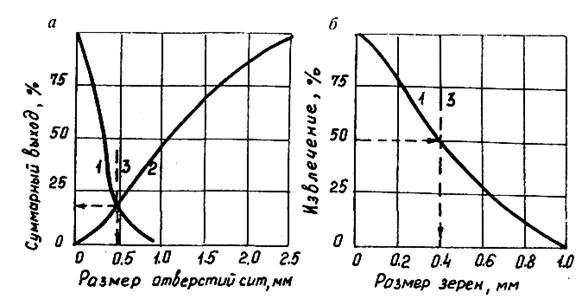
Рис. 2.7. Определение крупности разделения (3) при классификации по ре­зультатам ситового анализа слива (1) и песков (2)

 

При этом крупность разделения, по первому способу оп­ределяется абсциссой пересечения кривых гранулометричес­ких характеристик слива и песков (рис. 2.7, а). Данная круп­ность разделения отвечает размеру такого зерна, засоренность продуктов по которому одинакова. По второму способу (рис. 2.7, 6) за крупность разделения принимают размер зерна, извле­чение которого в слив и пески одинаково (равно 50 %). Эффек­тивность классификации определяют обычно по формуле Ханкока-Луйкена

.

 

 

Гидравлические классификаторы с восходящим потоком пульпы используются в основном при классификации строи­тельных материалов и для подготовки материала к гравита­ционному обогащению.

В классификаторе конструкции НИИЖелезобетона (рис. 2.8, а), используемом для получения песков при производстве бетона, питание подается сверху, навстречу восходящему по­току. Точность и эффективность классификации определяются производительностью. За рубежом для классификации строи­тельных песков широко используется классификатор «Реакс» (рис. 2.8,б).

Исходная пульпа в нем подается в среднюю часть, а вода — с двух сторон тангенциально в грушевидную полость ниж­ней части аппарата. Скорость восходящего потока по мере су­жения аппарата постепенно увеличивается. Частицы, конеч­ная скорость падения которых превышает скорость восходя­щего потока в зоне ввода пульпы, оседают и разгружаются че­рез отверстие внизу классификатора. Мелкие частицы выно­сятся вверх и разгружаются со сливом. Недостатками классификаторов являются: высокий расход воды (до 10 м³ на 1 т), большая высота аппаратов (до 15 м) и получение только двух продуктов — песков и слива.

В гидравлических многокамерных классификаторах (рис. 2.8, в), предназначенных для подготовки материала к гравита­ционному обогащению, материал разделяется на несколько продуктов (фракций). Для этого в каждой камере устанавли­вается своя скорость восходящего потока, значение которой понижается в направлении к разгрузочному порогу аппарата. Многокамерные классификаторы изготовляются четырехкамерными (КГ-4), шестикамерными (КГ-6) и восьмикамерными (КГ-8). Они представляют собой (см. рис. 3.8, в) открытый желоб 1, в дно которого вмонтированы пирамидальные клас­сификационные камеры 2 увеличивающего размера.

Рис. 2.8. Схемы гидравлических классификаторов:

а — конструкции НИИЖелезобетона; б — «Реакс»; в — многокамерного

 

Нижняя часть каждой камеры включает в себя классифика­ционную трубу 4, перемешивающее устройство (1—2 об/мин) для разрыхления взвеси песков 3, камеру для тангенциального ввода воды 5 и разгрузочное устройство 6. Достоинствами их являются: высокая точность классификации, автоматическая разгрузка песков и возможность регулировки процесса клас­сификации.

Для классификации в горизонтальном потоке использу­ются отстойники различной конструкции (элеваторные, пи­рамидальные и др.), классифицирующие конусы (песковые и шламовые) и механические классификаторы (спиральные, ре­ечные, чашевые, дражные и др.).

Наиболее простые из них элеваторные классификаторы (багер-зумпфы) применяют для предварительного обезвожи­вания мелкого концентрата и классификации его под действием силы тяжести по граничной крупности, равной примерно 0,5 мм; при этом пески удаляются из зумпфа элева­тором (рис. 2.9, а).

Автоматические конусные классификаторы (рис. 2.9, б) ис­пользуют для классификации зернистого материала (2—3 мм) при крупности разделения более 0,15 мм (в песковых конусах ККП) и шламистых материалов (менее 1 мм) при крупности разделения менее 0,15 мм (в шламовых конусах ККШ). Исход­ный продукт в них подается через центральную трубу, снаб­женную сеткой и успокоителем — рассекателем потока. Круп­ные зерна осаждаются, а тонкие частицы уходят в слив. При накоплении песков в конусе находящийся внутри него попла­вок поднимается, открывая клапан разгрузочного отверстия. Элеваторные и конусные классификаторы работают обычно без подачи дополнительной воды и эффективность их работы не­велика.

Рис. 2.9.Схемы багер-зумпфа (а), конусного (б) и спиральных классифи­каторов с непогруженной (в) и погруженной (г) спиралью

 

В механических классификаторах, наиболее часто исполь­зуемых в циклах измельчения для получения в сливе готового по крупности продукта, направляемого на обогащение, пески удаляются шнеком (в спиральных классификаторах), беско­нечной гребковой лентой со скребками или перфорирован­ными черпаками (в дренажных классификаторах) или рамой с гребками, совершающей возвратно-поступательное движение (в реечных классификаторах). Получивший преимущественное распространение спиральный классификатор (рис. 2.9, в) состо­ит из наклонного под углом 12-16° полуцилиндрического ко­рыта, в котором вращаются одна или две спирали из сталь­ных полос.

Исходный материал подается под уровень находящейся в классификаторе пульпы; крупные зерна осаждаются и тран­спортируются вращающейся спиралью к верхнему концу ко­рыта, а мелкие частицы уходят со сливом через сливной порог.

При крупности разделения 0,2 мм и выше применяют классификаторы с непогруженной спиралью (табл.2.1), в которых вся верхняя половина витка спирали выступает над зеркалом пульпы.

 

Таблица 2.1

Основные параметры классификаторов типа КСН (с непогруженной спиралью)

Показатели	1-КСН-3	1-КСН-5	1-КСН-7,5	1-КСН-10	1-КСН-12	1-КСН-15	1-КСН-17	1-КСН-20	1-КСН-24	2-КСН-24	1-КСН-24А	2-КСН-24А	1-КСН-24Б	1-КСН-30	2-КСН-30
Диметр спирали, мм
Длина спи- рали, мм
Количество спиралей, шт.
Частота			7,8		4,1	3,4	2,5	2,0	1,8	3,5	-	3,6	-	1,5	3,0
вращения вала спира­ли, мин-1					8,3	6,8	5,0	4,0
Угол уста- новки, град.						18,5								18,5	18,5
Мощность	1,1	1,1	3,0	5,5	5,5	7,5	10,0	13,0	13?0	22,0	22,0	40,0	22,0	30,0	40,0
эл.двигат.
привода спи­рали, кВт
Масса, т	0,8	1,5	3,0	5,0	7,0	13,0	17,0	19,0	23,0	37,0	34,0	57,0	39,0	42,0	70,0

 

Для получения более тонкого слива (более 65 % класса -0,074 мм) применяют классификаторы с погруженной спи­ралью (рис. 2.9, в, табл.2.2), в которых часть спирали у сливного порога целиком погружена в пульпу.

 

Таблица 2.2

Основные параметры классификаторов типа КСН (с погруженной спиралью)

 

Показатели	1-КСП-12	2-КСП-12	1-КСП-15	2-КСП-15	1-КСП-17	1-КСП-20	2-КСП-20	1-КСП-24	2-КСП-24	1-КСП-30
Диметр спирали, мм
Длина спирали, мм
Количество спиралей, шт.
Частота вращения вала спира­ли, мин-1	4,1	8,3	3,4	6,8	2,5	2,5	5,0	2,0	4,0	1,5 3,0
Угол установки, град.	15-18	15-18	15-18	15-18
Мощность электродвигателя привода спи­рали, кВт	5,5	10,0	7,5	10,1	-	13,0	22,0	13,0	30,0	30,0
Масса, т	10,5	17,0	19,0	32,0	25,0	31,0	56,0	35,0	63,5	60,0

 

Эффективность классификации составляет 35-65 %; ре­гулирование крупности слива производят изменением плотно­сти пульпы Т. По В.А. Олевскому, существует зависимость:

(3.29)

где β₇₄— содержание в сливе класса -0,074 мм, %.

Выбранный к установке классификатор должен обеспечивать требуемую производительность по сливу и пескам. Производительность (в т/ч) по сливу классификаторов с непогруженной спиралью определяется по формуле []

где m – число спиралей; Kβ– крупность слива (табл.2,3); Kδ– плотность материала; Kс– заданная плотность слива (табл.2,4); Kα– угол наклона днища классификатора (табл.2,5); D – диаметр спиралей, м (табл.2,6).

Производительность (в т/ч) по пескам определяется по формуле

где n – частота вращения спиралей, мин^-1; δ –плотность руды, т/м³.

Значения коэффициентов приведены в табл.2.3-2.6.

Таблица 2.3

Значения коэффициента Kβучитывающего крупность слива классификатора

Показатели	Номинальная крупность сливa d95, мм
	1,17	0,83	0,59	0,42	0,30	0,21	0,15	0,10	0,074
Содержание в сливе классов, %: - 0,074 мм - 0,044 мм		23 15
Базисное (условное) разжижение слива: Ж:Т по массе R2 твердого, %	1,3	1,5 40	1,6	1,8	2,0	2,33	4,0	4,5	5,7 16,5
Коэффициент Kβ	2,5	2,37	2,19	1,96	1,70	1,41	1,0	0,67	0,46

Таблица 2.4

Значения коэффициента К_с, учитывающего разжижение слива классификатора

Плотность руды δ, т/м3	Отношение RТ/R2,7
	0,4	0,6	0,8	1,0	1,2	1,5	2,0
2,7	0,60	0,73	0,86	1,0	1,13		1,67
3,0	0,63	0,77	0,93	,07	1,23	,44	1,82
3,3	0,66	0,82	0,98	,15	1,31	,55	1,97
3,5	0,68	0,85	1,02	,20	1,37	,63	2,07
4,0	0,73	0,92	1,12	,32	1,52	1,81	2,32
4,5	0,78	1 ,00	1,22	,45	1,66	,99	2,56
5,0	0,83	1,07	1,32	,57	1,81	2,18	2,81

 

Таблица 2.5

Значения коэффициента, учитывающего угол наклона днища классификатора

α°
Kα	1,12	1,10	1,06	1,03	1,0	0,97	0,94

Таблица 2.6

Величины D^1,765 и D³ для стандартных классификаторов

D, м	0,3	0,5	0,75	1,0	1,2	1,5	2,0	2,4	3,0
D1,765	0,12	0,27	0,6	1,0	1,38	2,04	3,40	4,70	6,97
D3	0,027	0,111	0,422	1,0	1,73	3,38	8,0	13,62	27,0

 

Классификацию в центробежном поле осуществляют в ги­дроциклонах и воздушных сепараторах.

Гидроциклоны (рис. 2.10, а, б) широко используются при классификации тонкодисперсных материалов различных по­лезных ископаемых, особенно при их измельчении.

 

Рис. 2.10. Схемы гидроциклона (а), трехпродуктового гидроциклона (б) и центробежного воздушного сепаратора (в)

 

Из многочисленных конструкций гидроциклонов на рудообогатительных фабриках применяют главным образом цилиндроконические с углом конусности 20° и малых типоразмеров с углом конусности 10°. В условное обозначение входят слово «гидроциклон», угол конусности (если он отличается от 20°), буквенные обозначения материала рабочих поверхностей гидроциклонов, диаметр гидроциклона (в мм) и обозначе­ние климатического исполнения (для стран с жарким климатом Т).

Пример: ГЦР-150, ГЦК-710, где Р - резина; К - каменное литьё.

Технологические характеристики гидроциклонов приведены в табл. 2.7.

При выборе и расчете гидроциклонов должны быть известны схе­мы измельчения и классификации, производительность мельницы по исходному питанию и её удельная производительность, циркулирующая нагрузка, характеристика крупности и содержание твердого в продукте измельчения, а также характеристики крупности продукта, поступаю­щего в цикл измельчения.

 

 

Таблица 2.7

Основные параметры классифицирующих гидроциклонов

Диаметр гидроци-клона D, мм	Угол конусно-сти α, град.	Средняя производитель­ность Vn, м3/ч (приР0=0,1МПа)	Круп-ность слива dн(при ρт=2,7 г/см3)	Стандартный эквивал. диаметр питающего отверстия dн, мм	Стандартный диаметр сливного патрубка d, мм	Диаметр песковой насадки Δ, мм
		0,15-0,3	-			-
		0,45-0,9	-			4-8
		1,8-3,6				6-12
		3-10	10-20	15-20	18-25	8-17
	10,20	12-30	20-50	30-40	40-50	12-34
		27-80	30-100			24-75
		50-150	40-150			34-96
		100-300	50-200			48-150
		200-500	60-250			48-200
		360-1000	70-280			75-250
		700-2000	80-300			150-300
		1100-3800	90-330			250-500

 

Расчет гидроциклонов начинают с расчета количественной и шла­мовой схемы, т. е. с определения производительности каждого продукта по твердому, по количеству воды и пульпы. По условиям классифика­ции предварительно выбирается гидроциклон определенного типораз­мера (Д). Необходимое давление пульпы на входе в гидроциклон (P₀) определяется по формуле [3,4]

где V— производительность, м³/ч;

К_α - поправка на угол конусности гидроциклона (α = 10°, К_α= 1,15; α= 20°,

К_α = 10);

К_D- поправка на диаметр гидроциклона (табл.2.8);

d_п- эквивалентный диаметр питающего отверстия, см;

d - диаметр сливного патрубка, см.

 

 

Таблица 2.8

Значения коэффициента К₀для расчета гидроциклона

Диаметр гидроциклона D, см
Поправочный коэффициент КD	1,28	1,14	1,06	1,0	0,95	0,91	0,88	0,81
Высота гидроциклона, Hг„м	-	-	-	-	3,5	4,5

 

Для гидроциклонов диаметром больше 500 мм необходимо учиты­вать высоту гидроциклона [3,4]:

(2.35)

где Р_t- давление, создаваемое насосом на входе в гидроциклон, МПа;

Н_г— высота гидроциклона, м;

ρ_п — плотность исходной пульпы, г/см³.

У выбранного типоразмера гидроциклона проверяется величина на­грузки на песковое отверстие и её соответствие норме (0,5-2,5 г/ч • см²) по формуле [3,4]

(2.36)

где Q_п — производительность по пескам, т/ч;

S_n— площадь пескового отверстия, см².

Проверка номинальной крупности d_n слива гидроциклона произво­дится по формуле [3,4]

(2.37)

где β_п^тв - содержание твердого в исходной пульпе (табл.2.39), %;

Δ - диаметр пескового отверстия (насадка), см;

ρ_т и ρ — плотность твердой и жидкой фаз, г/см³.

 

Таблица 2.9

Зависимость содержания твердого в песках гидроциклона от крупности слива

Содержание класса -0,074 мм в сливе, βс-74, %	50-60	60-70	70-80	80-85	85-90	90-95	95-100
Содержание твердого в песках, Βптв, %
Разжижение песков Т:Ж	0,25	0,33	0,39	0,43	0,43	0,49	0,54

 

Исходная пульпа под давлением от 5 до 50 Н/см² (0,5— 5 кгс/см²) подается через патрубок тангенциально к внутрен­ней поверхности цилиндрической части гидроциклона и прио­бретает в нем вращательное движение.

Тяжелые и крупные частицы под действием центробеж­ной силы отбрасываются к стенкам аппарата и нисходящим спиральным потоком движутся вниз, разгружаясь через насад­ку для песков. Мелкие же частицы вместе с основной массой воды образуют внутренний поток, который поднимается вверх, и выносится через сливной патрубок.

Трехпродуктовый гидроциклон (см. рис. 2.10, б) имеет двой­ную сливную трубу. Крупность слива возрастает с увеличени­ем плотности и вязкости исходного материала и с уменьше­нием диаметра песковой насадки. Большое влияние на эффек­тивность разделения оказывает отношение диаметров песко­вой насадки и сливного патрубка, равное обычно 0,5-6,6. Диаметр сливного патрубка составляет 0,2-0,4 диаметра цилиндрической части гидроциклона, размер которой дости­гает 1500 мм. Для получения тонких сливов (менее 5-10 мкм) применяют батареи из гидроциклонов диаметром 15-100 мм, работающих при давлении пульпы на входе в гидроциклоны до 90 Н/см² (9 кгс/см²). Преимуществами гидроциклонов яв­ляются простота конструкции, отсутствие движущих частей, малые размеры; недостатками — повышенный износ внут­ренней поверхности корпуса и насадок, для предотвращения чего их футеруют каменным литьем или гуммируют.

В центробежных воздушных сепараторах (рис. 2.10, в) вра­щающаяся тарелка разбрасывает исходный материал во вну­тренней камере. Крупные зерна оседают в воронке, а тонкий продукт выносится потоком воздуха и оседает во внешней ка­мере. Крупность разделения регулируют скоростью воздушно­го потока.