Минимизация числа внутренних состояний автомата

Под минимизацией числа внутренних состояний автомата понимается процесс, целью которого является получение автомата имеющего минимальное число внутренних состояний среди всех автоматов, реализующих заданные условия работы. Условиями работы автомата будем называть множество пар - входное слово и реакция автомата.

Будем говорить, что две последовательности А=а1…..аi и В=b1….bi являются непротиворечивыми, если в них не содержится ни одной пары элементов [аi, bi] таких, что и .

Говорят, что автомат реализует заданные условия работы, то есть является реализующим автоматом, если при поступлении на его вход входной последовательности на выходе автомата будет выдаваться выходная последовательность, непротиворечивая последовательности, задаваемой условиями работы автомата. Два автомата, реализующие одни и те же условия работы, будем называть эквивалентными автоматами. Одни и те же условия работы могут реализовать несколько эквивалентных автоматов, имеющие различное число внутренних состояний. Задача минимизации состоит в выявлении среди этих эквивалентных автоматов минимального. Поскольку, число внутренних состояний автомата определяет ёмкость памяти, процесс минимизации числа внутренних состояний автомата приводит к минимизации числа элементов памяти.

Имеется соотношение:

,

где М – число внутренних состояний, которые может хранить ЭП,

N – количество внутренних состояний автомата.

 

Сокращение числа внутренних состояний целесообразно производить, т.к. это приводи (в большинстве случаев) к уменьшению числа элементов памяти и упрощению структуры логического преобразователя. Однако необходимо помнить, что сокращение числа внутренних состояний до минимального может привести к возникновению гонок.

В настоящее время существует две группы методов построения автомата с минимальным числом внутренних состояний. Для первой группы характерно то, что сначала берётся автомат с одним внутренним состоянием, а затем производится увеличение числа его внутренних состояний до тех пор, пока он не станет реализующим автоматом.

Во второй группе методов берётся заведомо реализующий автомат с каким-то числом внутренних состояний, а затем производится уменьшение внутренних состояний до тех пор, пока автомат при числе внутренних состояний (N-1) не станет нереализующим.

Методы минимизации первой группы нашли применение при задании автомата таблицами включений. Методы второй группы применяются, когда автомат задан другими стандартными способами.

Для минимизации числа внутренних состояний недоопределенного автомата в настоящее время отсутствует простой алгоритмизированный метод, дающий возможность получить минимальный недоопределенный автомат. Перебор всех возможных вариантов с целью выбора из них минимального автомата становиться невозможным, даже для автомата с относительно небольшим числом внутренних состояний. В связи с трудностью синтеза минимального недоопределенного автомата в настоящее время в данной области наметились две тенденции:

1. Разработка приближённых, но алгоритмизуемых методов, которые не гарантируют построение минимального реализующего автомата, но позволяют запрограммировать данный процесс. Метод Е.А. Бутакова.

2. Разработка методов минимизации отдельных частных классов недоопределённых автоматов, для которых имеется возможность построения минимального автомата.

 

12. Минимизация полностью определённых автоматов.

Рассмотрим метод, предположенный Ауфенкампом и Хоном.

Основная идея этого метода состоит в разбиении всех состояний исходного абстрактного автомата на попарно непересекающиеся классы эквивалентных состояний и замене каждого класса эквивалентности одним состоянием. Получающийся в результате минимальный автомат имеет столько же состояний, на сколько классов эквивалентности разбивается множество состояний исходного автомата.

Два состояния абстрактного автомата xm и xs называются эквивалентными, если выходная функция для всех возможных входных слов Ф. Иначе состояния называются неразличимыми.

Более слабой формой эквивалентности является k-эквивалентность:

для всех возможных слов длиной k.

Введённые отношения эквивалентности симметричны, транзитивны и рефлексивны. Следовательно, они могут быть использованы для разбиения множества состояний абстрактного автомата на попарно непересекающиеся классы – классы эквивалентности. Соответствующие разбиения на классы эквивалентности и k-эквивалентности будем обозначать через и . Разбиение позволяет определить избыточные элементы в множестве внутренних состояний. Если каждый класс эквивалентности содержит только одно состояние, то множество внутренних состояний не сократимо.

Рассмотрим алгоритм минимизации числа внутренних состояний полностью определённого автомата:

1. Находятся последовательные разбиения , множества X до тех пор, пока на каком-то (k+1) шаге не окажется, что это разбиение ничем не отличается от предыдущего. Доказано, что в этом случае (=) есть необходимое нам разбиение, и дальнейшее сокращение числа внутренних состояний автомата невозможно.

2. В каждом классе эквивалентности разбиения выбирается по одному элементу, который образует множество X’.

3. Функции переходови функция выходов для автомата определяются на множестве оставшихся внутренних состояний и множестве входных сигналов. Для этого в таблице переходов вычеркиваются столбцы, соответствующие состояниям, не вошедшим в множество , а в оставшихся столбцах таблицы переходов все состояния заменяются на эквивалентные из множества . В таблице выходов столбцы вычёркиваются.

4. В качестве начального состояния выбирается одно из состояний, эквивалентных X0. На практике лучше взять само X0.

ПРИМЕР:

Минимизация полного автомата Мили:

Таблица переходов:

X1 X2 X3 X4 X5 X6 X7 X8 X9 X10 X11 X12
1 X10 X12 X5 X7 X3 X7 X3 X10 X7 X1 X5 X2
2 X5 X8 X6 X11 X9 X11 X6 X4 X6 X8 X9 X8

 

Таблица выходов:

X1 X2 X3 X4 X5 X6 X7 X8 X9 X10 X11 X12
1 1 1 2 2 1 2 1 1 2 2 2 2
2 2 2 1 1 2 1 2 2 1 1 1 1

={X1,X2,X5,X7,X8} B1,

{X3,X4,X6,X9,X10,X11,X12 } B2

 

X1 X2 X5 X7 X8 X3 X4 X6 X9 X10 X11 X12
1 B2 B2 B2 B2 B2 B1 B1 B1 B1 B1 B1 B1
2 B1 B1 B2 B2 B2 B2 B2 B2 B2 B1 B2 B1

={X1,X2} C1,

{X5,X7,X8} C2,

{X3,X4,X6,X9,X11} C3,

{X10,X12}C4,

 

X1 X2 X5 X7 X8 X3 X4 X6 X9 X11 X10 X12
1 C4 C4 C3 C3 C4 C2 C2 C2 C2 C2 C1 C1
2 C2 C2 C3 C3 C3 C3 C3 C3 C3 C3 C2 C2

={X1,X2} D1,

{X5,X7} D2

{X8} D3

{X3,X4,X6,X9,X11} D4

{X10,X12} D5

 

Соответственно, получили разбиение, для которого дальнейшее разбиение невозможно.

Произвольно выбираем из каждого класса по одному состоянию и формируем множество

 

X1 X3 X5 X8 X10
1 X10 X5 X3 X10 X1
2 X5 X3 X3 X3 X8
X1 X3 X5 X8 X10
1 1 2 1 1 2
2 2 1 2 2 1

 

Особенности минимизации для автомата Мура.

1 1 3 3 3 2 3 1 2 2 2 2
X1 X2 X3 X4 X5 X6 X7 X8 X9 X10 X11 X12
1 X10 X12 X5 X7 X3 X7 X3 X10 X7 X1 X5 X2
2 X5 X7 X6 X11 X9 X11 X6 X4 X6 X8 X9 X8

 

При минимизации автомата Мура вводится понятие 0-эквивалентности и, соответственно, разбиения множества внутренних состояний на 0- эквивалентные классы. 0- эквивалентными называются любые одинаково отмеченные состояния автомата Мура. Если два 0- эквивалентных состояния любыми входными сигналами переводятся в два 0- эквивалентных состояния, то они называются 1-экивавлентными состояниями.

={X1,X2,X8} А1

{X3,X4,X5,X7} A2

{X6,X9,X10,X11,X12} А3

13. Совмещённая модель автомата (C-автомата )

Под абстрактным С-автоматом будем понимать математическую модель С-устройства, определяемую множеством из восьми элементов.

 
 

 

 


С-автомат можно представить в виде устройства с одним входом и двумя выходами. Отличие С-автомата от автоматов Мили и Мура состоит в том, что он реализует функции выходов, как для автомата Мили, так и для автомата Мура.

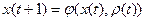
Очевидно, что от С-автомата легко перейти к автомату Мили или к автомату Мура.

В ряде случаев, оказывается, удобно использовать С-автомат для проектирования различных узлов вычислительной техники.

Для задания С-автомата также используются табличные, матричный и графовый способы. Таблица переходов С-автомата аналогична таблице переходов автомата Мили. В таблице выходов С-автомата каждое состояние отмечено соответствующим ему выходным сигналом типа U.

ПРИМЕР:

Таблица переходов:

X1 X2 X3 X4
1 X2 X3 X1 X2
2 X4 X2 X1 X3

 

Таблица выходов:

U1 U2 U1 U3
X1 X2 X3 X4
1 1 2 1 2
2 2 2 1 2

При задании С-автомата в виде графа выходные сигналы типа приписываются дугам графа, а сигнал типа u приписывается вершинам состояний, которым эти сигналы соответствуют.

 

Нетрудно доказать, что к полностью определённому С-автомату можно применить алгоритм минимизации Ауфенкампа.

Под 1-эквивалентным состоянием С-автомата необходимо понимать состояния, которые одинаково отмечены и имеют одинаковые столбцы в таблице выходов. Дальнейшее разбиение на классы эквивалентности происходит аналогично минимизации автомата Мили.