Переход от автомата Мили к автомату Мура и обратно
Матричный способ задания автоматов
Задание автомата с помощью графа
Таблица выходов.
Таблица переходов.
Табличный способ задания автоматов
Способы задания автоматов
Для задания автоматов существуют специальные формализованные языки.
Словесное описание поведения автоматов без рассмотрения внутреннего устройства позволяет описать алгоритм, который задает отображение последовательности состояний входа и состояний выхода автомата. Автомат в этом случае задается как черный ящик, и функции переходов в явном виде не описываются, такие языки получили название начальные.
К начальным языкам относятся: язык регулярных выражений, язык предикатных форм, язык логических схем алгоритма. Широкого применения эти языки не нашли. Для описания частного класса автомата оказался удобным начальный язык логических схем алгоритмов НЯЛСА.
Если рассматривать автомат с учетом его внутренних состояний, то необходимо определить функции перехода (из внутреннего состояния xi во внутреннее состояние xj не исключая i=j). Задание функций выходов означает, что каждой паре 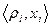 поставлено в соответствие состояние выхода
поставлено в соответствие состояние выхода 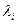 .
.
Языки позволяющие таким образом описать автомат называются стандартными языками. К стандартным относятся таблицы переходов, таблицы выходов, матрицы переходов, таблицы включений, графы переходов.
Каждая строка (столбец) таблицы переходов соответствует состоянию входов, а каждый столбец (строка) внутреннему состоянию.
| X1 | X2 | X3 | X4 | |
 1 1
| X2 | X1 | X1 | X2 |
 2 2
| X3 | X3 | X1 | X4 |
 3 3
| X4 | X2 | X1 | X1 |
Каждая клетка соответствует внутреннему состоянию автомата, в который он должен перейти в следующий момент времени. Если в автомате какое либо состояние не определено, то в соответствующей клетке ставится прочерк. Прочерк означает, что либо это состояние запрещено, либо дальнейшее поведение не определено.
Например, задан автомат, для которого не может быть подано двух одинаковых входных сигналов следующих друг за другом.
 1 1
|  2 2
| |
| X1 | X1 | X2 |
| X2 | X3 | - |
| X3 | - | X4 |
| X4 | X1 | - |
Функция выхода автомата также может быть задана в виде таблицы. При этом вид таблицы зависит от модели автомата (Мили, Мура).
Для автомата Мили столбцы соответствуют внутренним состояниям, строки – входным сигналам, в ячейках – выходные сигналы.
| X1 | X2 | X3 | |
 1 1
|  1 1
|  3 3
|  1 1
|
 2 2
|  2 2
|  3 3
|  1 1
|
 3 3
|  1 1
|  2 2
|  1 1
|
Запись  1 означает, что если подать на вход автомата, находящегося в состоянии Х1, сигнал
1 означает, что если подать на вход автомата, находящегося в состоянии Х1, сигнал  1, то на выходе будет
1, то на выходе будет  1.
1.
Для автомата Мура таблица выходов не строится, т.к. от выходной сигнал не зависит от входного. Для автомата Мура строится совмещенная таблица переходов и выходов
 1 1
|  2 2
|  1 1
| |
| Х1 | Х2 | Х3 | |
 1 1
| X1 | X2 | X3 |
 2 2
| X1 | - | X2 |
 3 3
| - | Х3 | - |
Табличный способ для асинхронного автомата
Как и для синхронного автомата, каждая ячейка таблицы переходов асинхронного автомата соответствует внутреннему состоянию, в которое перейдет автомат. Это состояние определяется внутренним состоянием в предыдущий момент времени и поданным на вход сигналом.
Устойчивое состояние асинхронного автомата, т.е. состояние, соответствующее устойчивому такту обозначается в таблице переходов круглыми скобками. Неустойчивое состояние - записывается без скобок.
 1 1
|  2 2
|  3 3
| |
| X1 | X2 | X2 | Х3 |
| X2 | X3 | (Х5) | (Х2) |
| X3 | Х6 | - | (Х1) |
| X4 | - | Х1 | Х3 |
| Х5 | (Х1) | Х6 | Х4 |
| Х6 | (Х4) | - | Х6 |
Входной сигнал можно менять, когда автомат перешел в новое устойчивое состояние. Если устойчивого состояния нет, то происходит зацикливание (неустойчивое состояние).
Если автомат переходит из одного устойчивого внутреннего состояния под воздействием входного сигнала в другое состояние, то входной сигнал можно изменять только при «попадании» автомата в устойчивое состояние. Переход автомата из одного устойчивого состояния в другое устойчивое может осуществляться через несколько неустойчивых состояний.
Таблица выходов.Особенность для асинхронных автоматов состоит в том, что записывается последний выходной сигнал (при устойчивом состоянии). В столбце внутренних состояний записываются только устойчивые состояния. Выходные сигналы соответствуют устойчивому состоянию.
 1 1
|  2 2
| |
| X1 |  1 1
|  1 1
|
| X2 |  2 2
| - |
| X3 |  2 2
|  3 3
|
| X4 | - |  1 1
|
Граф автомата – это связный граф, вершины которого соответствуют внутренним состояниям автомата, а дуги определяют переходы между состояниями.
Для автомата Мили:
Две вершины графа автомата xi и xj соединяются дугой, направленной от xi к xj, если в автомате имеется переход из состояния xi в состояние xj. Дуге графа приписывается входной сигнал  и выходной сигнал
и выходной сигнал  . Если переход автомата из состояния xi в состояние xj происходит под воздействием нескольких входных сигналов, то дуге приписываются все эти сигналы через знак v (дизъюнкции).
. Если переход автомата из состояния xi в состояние xj происходит под воздействием нескольких входных сигналов, то дуге приписываются все эти сигналы через знак v (дизъюнкции).
Пример:
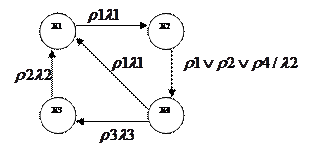 |
Для автомата Мура:
В автомате Мура выходной сигнал зависит только от внутреннего состояния автомата, поэтому он приписывается вершинам графа, соответствующим определенному внутреннему состоянию автомата. Все остальное как и в автомате Мили.
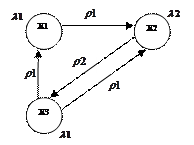 |
Для асинхронного автомата.
Особенностью графа асинхронного автомата является следующее: для того чтобы автомат поддерживал себя в устойчивом состоянии до тех пор пока не придет новый входной сигнал, необходимо указать дугу, зацикливающую вершину саму на себя с тем же входным сигналом.
 |
Матрица переходов представляет собой квадратную матрицу, строки и столбцы которой соответствуют внутренним состояниям автомата.
Элементы [i,j] указывают состояние входа автомата  , при котором он переходит из внутреннего состояния xi в состояние xj, и состояние выхода, которое соответствует полному состоянию М. В каждой строке матрицы перехода одно и тоже состояние входа
, при котором он переходит из внутреннего состояния xi в состояние xj, и состояние выхода, которое соответствует полному состоянию М. В каждой строке матрицы перехода одно и тоже состояние входа  не может встретиться более одного раза. Если автомат из внутреннего состояния xi переходит в состояние xj под воздействием нескольких входных сигналов, то в соответствующей ячейке проставляется дизъюнкция состояния входа.
не может встретиться более одного раза. Если автомат из внутреннего состояния xi переходит в состояние xj под воздействием нескольких входных сигналов, то в соответствующей ячейке проставляется дизъюнкция состояния входа.
| X1 | X2 | X3 | |
| X1 |  1 1 2 2
|  2 2 1 1
| - |
| X2 |  1v 1v 3/ 3/ 2 2
| - |  2 2 3 3
|
| X3 | - | - |  2 2 1 1
|
Абстрактный автомат может работать, как некоторый преобразователь входного слова в слова выходного алфавита
Пусть на вход этого автомата поступает входное слово – 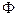 (последовательность входных сигналов).
(последовательность входных сигналов).
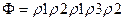
Назовем переменную 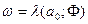 реакцией автомата, находящегося в состоянии а0, на входное слово
реакцией автомата, находящегося в состоянии а0, на входное слово 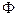 .
.
Автомат Мили в ответ на входное слово длиной k выдает последовательность состояний длиной k+1 и выходное слово длиной k.
Зададим автомат Мура.
Найдем реакцию автомата Мура на входное слово – 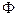 . Начальное состояние x1:
. Начальное состояние x1:
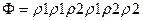
x1x4x2x1x4x3x5
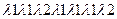
Два автомата SА и SB с одинаковыми входным и выходным алфавитом называются - эквивалентными, если после установления их в начальное состояние реакции на любое входное слово совпадают.
Можно показать, что для любого автомата Мили существует эквивалентный ему автомат Мура, и наоборот. При написании алгоритма взаимной трансформации часто пренебрегают выходным сигналом, связанным с начальным состоянием.
Рассмотрим переход от автомата Мура к автомату Мили.
Пусть задан автомат Мура:
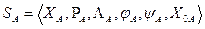
Необходимо построить автомат Мили, эквивалентный автомату Мура:


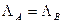
Функцию  определим следующим образом: если в автомате Мура имеются функции
определим следующим образом: если в автомате Мура имеются функции 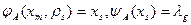 , то для автомата Мили можно записать следующую функцию выхода:
, то для автомата Мили можно записать следующую функцию выхода: 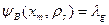 .
.
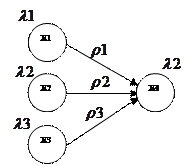
Рассмотрим переход от автомата Мура к автомату Мили с помощью графа:
Для осуществления перехода от автомата Мура к автомату Мили выходной сигнал  , находящийся в автомате Мура рядом с вершиной, для автомата Мили передается на все дуги, входящие в эту вершину.
, находящийся в автомате Мура рядом с вершиной, для автомата Мили передается на все дуги, входящие в эту вершину.
 | |||
 |
Переход от автомата Мура к Мили табличным способом:
Поскольку таблица переходов автомата Мура полностью совпадает с таблицей переходов автомата Мили, то основная проблема при описании автомата Мили табличным способом – это составление таблицы выходов. Таблица выходов автомата Мили получается из таблицы переходов автомата Мура путем замены символа соответствующего внутреннему состоянию автомата Мура символом выходного сигнала.
Для автомата Мура
 1 1
|  2 2
|  3 3
| ||
 1 1
| X1 | X1 | X2 | X4 |
 2 2
| X2 | X2 | X3 | X1 |
 1 1
| X3 | X1 | X3 | X4 |
 3 3
| X4 | X1 | X1 | X4 |
Для автомата Мили
 1 1
|  2 2
|  3 3
| |
| X1 | 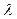 1 1
| 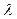 2 2
| 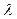 3 3
|
| X2 | 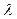 2 2
| 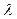 1 1
| 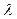 1 1
|
| X3 | 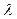 1 1
| 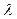 1 1
| 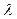 3 3
|
| X4 | 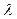 1 1
| 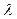 1 1
| 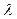 3 3
|
Из самого способа построения автомата Мили очевидно, что он эквивалентен автомату Мура.
Для входной последовательности Ф поведение автоматов Sа и полностью совпадают. По индукции не трудно доказать, что любое входное слово конечной длины, поданное на входы автоматов Sа и SВ, установленных в начальное состояние x0 вызовет появление одинаковых выходных слов.
Переход от автомата Мили к автомату Мура. При переходе от автомата Мили к автомату Мура необходимо наложить следующие ограничения: в автомате Мили не должно быть преходящих состояний.
Преходящее состояние - это состояние, в которое при представлении автомата в виде графа не входит ни одна дуга и которое имеет хотя бы одну выходящую дугу.
Задан автомат Мили Sа . Необходимо построить автомат Мура SВ.
Алфавиты должны совпадать:

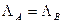
Для определения множества XB каждому состоянию  поставим соответствующее множество пар вида
поставим соответствующее множество пар вида 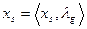 ,где
,где 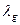 -это выходной сигнал приписанный дуге, входящей в xs.
-это выходной сигнал приписанный дуге, входящей в xs.
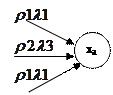 |

Число элементов в множестве XS будет равно числу различных выходных сигналов на дугах автомата Мили SA, входящих в состояние xa Число внутренних состояний автомата Мура будет определяться объединением множеств всех XS.

XA => XB
Функция переходов 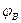 и функция выходов
и функция выходов  определяется так: если в автомате Мили имеется переход из состояния xm в состояние xs под воздействием
определяется так: если в автомате Мили имеется переход из состояния xm в состояние xs под воздействием 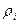
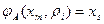
и при этом выдается выходной сигнал 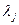
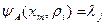 ,
,
то в автомате Мура будет переход из множества состояний X’m, порождаемое внутренним состоянием xm под воздействием входного сигнала 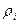 .
.
 .
.
Функция выходов автомата Мура определяется следующим образом

В качестве начального состояния x0B можно взять любое состояние из множества, которое порождается начальным состоянием x0А.
 Т.о. получается автомат SВ, эквивалентный автомату SA.
Т.о. получается автомат SВ, эквивалентный автомату SA.
 |
Автомат Мили Автомат Мура
Изложенные методы взаимных транспозиций модели Мили и Мура показывают, что при переходе от автомата Мура к Мили число состояний автомата не меняется, а при обратном переходе число состояний, как правило, возрастает.
Вследствие транзитивности отношения эквивалентности  . Два автомата Мили также будут эквивалентны, хотя у последнего на два состояния больше. Таким образом, эквивалентные автоматы могут иметь различное число внутренних состояний. В связи с этим возникла задача нахождения минимального автомата в классе эквивалентных между собой автоматов.
. Два автомата Мили также будут эквивалентны, хотя у последнего на два состояния больше. Таким образом, эквивалентные автоматы могут иметь различное число внутренних состояний. В связи с этим возникла задача нахождения минимального автомата в классе эквивалентных между собой автоматов.