Этап Построение линий уровня целевой функции и определение точки максимума
Цель - найти в построенном многоугольнике AFEDCB точку, в которой функция цели Z=2x1 + 3x2 принимает максимальное значение.
Проведем прямую 2x1 + 3x2 = Сonst (линию уровня) так, чтобы она пересекала многоугольник AFEDCB (например, Const=10). Эта линия уровня на рисунке изображена пунктирной линией.
Если рассматривать значения линейной целевой функции Z на множестве точек (x1,x2), принадлежащих отрезку пунктирной прямой, расположенному внутри шестиугольника, то все они равны одному и тому же значению (Const=10).
Определим направление возрастания функции. Для этого построим линию уровня с бОльшим значением. Это будет прямая, параллельная с построенной, но расположенная правее. Значит, в заданном направлении значение целевой функции возрастает, и в наших интересах сдвинуть ее как можно дальше в этом направлении.
Сдвиг можно продолжать до тех пор, пока перемещаемая прямая пересекает многоугольник допустимых решений. Последнее положение прямой, когда она имеет одну общую точку с многоугольником AFEDCB (точка С), соответствует максимальному значению целевой функции Z и достигается в точке С с координатами x1= 4/3 (»1.333), x2 =10/3 (»3.333). При этом Z = 38/3 ( »12.667).
Поставленная задача полностью решена. Из проведенных геометрических рассуждений видно, что решение единственное. Сделаем некоторые обобщения, вытекающие из геометрической интерпретации задачи.
Первое. Область допустимых решений – выпуклый многоугольник (Почему выпуклый? Может ли область допустимых решений представлять собой пустое множество? Точку? Отрезок? Луч? Прямую? Если да, приведите пример системы ограничений).
Второе.Максимум целевой функции достигается в вершине многоугольника допустимых решений
47. условие оптимальности решения задач линейного программирования
Суть принципа оптимальности состоит в стремлении выбрать такое планово-управленческое решение  , где
, где 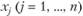 - его компоненты, которое наилучшим образом учитывало бы внутренние возможности и внешние условия производственной деятельности хозяйствующего субъекта.
- его компоненты, которое наилучшим образом учитывало бы внутренние возможности и внешние условия производственной деятельности хозяйствующего субъекта.
Слова "наилучшим образом" здесь означают выбор некоторого критерия оптимальности, т.е. некоторого экономического показателя, позволяющего сравнивать эффективность тех или иных планово-управленческих решений. Традиционные критерии оптимальности: "максимум прибыли", "минимум затрат", "максимум объема работ (услуг)" и др.
Слова "учитывало бы внутренние возможности и внешние условия производственной деятельности" означают, что на выбор управленческого решения (поведения) накладывается ряд условий, т.е. выбор  осуществляется из некоторой области возможных (допустимых) решений D; эту область называют также областью определения задачи.
осуществляется из некоторой области возможных (допустимых) решений D; эту область называют также областью определения задачи.
Таким образом, реализовать на практике принцип оптимальности в планировании и управлении - это значит решить экстремальную задачу вида
 (2.1)
(2.1)
 (2.2)
(2.2)
где  - математическая запись критерия оптимальности - целевая функция задачи (модели) оптимизации.
- математическая запись критерия оптимальности - целевая функция задачи (модели) оптимизации.
Задачу условной оптимизации (2.1), (2.2) обычно записывают в виде:
найти максимум или минимум функции
 (2.3)
(2.3)
при ограничениях
 (2.4)
(2.4)
………………………..
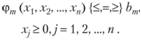 (2.5)
(2.5)
Условие (2.5) необязательно, но его всегда при необходимости можно добиться. Обозначение {≤,=,≥} говорит о том, что в конкретном ограничении возможен один из знаков ≤, = или ≥. Более компактная запись:
 (2.6)
(2.6)
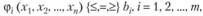 (2.7)
(2.7)
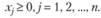 (2.8)
(2.8)
Задача (2.6)-(2.8) - общая задача оптимального (математического) программирования, иначе - математическая модель задачи оптимального программирования, в основе построения (разработки) которой лежат принципы оптимальности, системности и адекватности.
Вектор  (набор управляющих переменных хj, j = 1, 2, ..., п) называется допустимым решением или планом задачи оптимального программирования, если его компоненты xj удовлетворяют системе ограничений. А тот план
(набор управляющих переменных хj, j = 1, 2, ..., п) называется допустимым решением или планом задачи оптимального программирования, если его компоненты xj удовлетворяют системе ограничений. А тот план 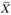 (допустимое решение), который доставляет максимум или минимум целевой функции f(x1, х2, ..., хn) называется оптимальным планом (оптимальным поведением, или просто решением) задачи оптимального программирования.
(допустимое решение), который доставляет максимум или минимум целевой функции f(x1, х2, ..., хn) называется оптимальным планом (оптимальным поведением, или просто решением) задачи оптимального программирования.
Таким образом, выбор оптимального управленческого поведения в конкретной производственной ситуации связан с проведением с позиций системности, адекватности и оптимальности экономико-математического моделирования и решением задачи оптимального программирования.
Решить задачу оптимального программирования (получить решение по оптимизационной экономико-математической модели) - это значит:
- во-первых, найти оптимальный план 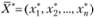 ,
,
который, с учетом интерпретации его компонент, и определяет оптимальное поведение в рассматриваемой ситуации;
- во-вторых, найти оптимальное значение (максимум или минимум) целевой функции  , которое и представляет собой экономическую оценку последствий предлагаемого решения (поведения).
, которое и представляет собой экономическую оценку последствий предлагаемого решения (поведения).
Иногда невозможно получить решение по оптимизационной модели: область допустимых решений может оказаться пустым множеством (задача противоречива) или целевая функция является неограниченной на области определения.
Первый случай связан с некорректностями в постановке экономической задачи или (и) разработанной экономико-математической модели (ЭММ). Например, с имеющимся объемом ресурсов заведомо невозможно выполнить даже те минимальные объемы работ, которые закладываются в ограничения как необходимые минимальные плановые задания. Если в данной ситуации все же необходимо найти решение задачи, то следует построить непустое множество допустимых решений, исключив одно или несколько ограничений, т.е. фактически соблюсти принцип альтернативности.
Второй случай обычно означает, что ЭММ разработана некорректно и некоторые существенные ограничения в ней отсутствуют.
Задачи оптимального программирования в наиболее общем виде классифицируют по следующим признакам.
1. По характеру взаимосвязи между переменными:
а) линейные;
б) нелинейные.
В случае (а) все функциональные связи в системе ограничений и функция цели - линейные функции, наличие нелинейности в хотя бы одном из упомянутых элементов приводит к случаю (б).
2. По характеру изменения переменных:
а) непрерывные;
б) дискретные.
В случае (а) значения каждой из управляющих переменных могут заполнять сплошь некоторую область действительных чисел, в случае (б) все или хотя бы одна переменная могут принимать только целочисленные значения.
3. По учету фактора времени:
а) статические;
б) динамические.
В задачах (а) моделирование и принятие решений осуществляются в предположении о независимости от времени элементов модели в течение периода времени, на который принимается планово-управленческое решение. В случае (б) такое предположение достаточно аргументированно принято не может быть и необходимо учитывать фактор времени.
1. По наличию информации о переменных:
а) задачи в условиях полной определенности (детерминированные);
б) задачи в условиях неполной информации;
в) задачи в условиях неопределенности.
В задачах (б) отдельные элементы являются вероятностными величинами, однако известны или дополнительными статистическими исследованиями могут быть установлены их законы распределения вероятностей. В случае (в) можно сделать предположение о возможных исходах случайных элементов, но нет возможности сделать вывод о вероятностях исходов.
return false">ссылка скрыта2. По числу критериев оценки альтернатив:
а) простые, однокритериальные задачи;
б) сложные, многокритериальные задачи.
В задачах (а) экономически приемлемо использование одного критерия оптимальности или удастся специальными процедурами (например, "взвешиванием приоритетов") свести многокритериальный поиск к однокритериальному; примеры многокритериальных задач рассмотрены в главе 3.
Сочетание признаков 1-5 позволяет группировать (классифицировать) в самом общем виде задачи и методы оптимального программирования, например: 1а)2а)3а)4а)5а) - задачи и методы линейного программирования, 1б)2а)3а)4а)5а) - задачи и методы нелинейного программирования, 1а)2б)3а)4а)5а) - задачи и методы целочисленного (дискретного) линейного программирования и т.д.
Новые возможности для широкого практического применения методов оптимального программирования представляют современные офисные средства. Широкий круг специалистов в своей повседневной практике использует необходимый компонент финансово-экономических расчетов - Microsoft Excel (MS Excel), который содержит специальное средство - надстройку Поиск решения,позволяющую реализовывать модели линейной, нелинейной и дискретной оптимизации. Технология оптимизации с помощью надстройки Поиск решенияс решением некоторых типовых задач оптимального программирования в среде MS Excel подробно рассмотрена, например, в литературе.
48. Основные определения теории двойственности.
Каждой задаче линейного программирования можно поставить в соответствие другую задачу линейного программирования. При решении одной из них автоматически решается и другая задача. Такие задачи называют взаимодвойственными. Покажем, как по данной задаче (будем называть ее исходной) построить двойственную ей.
Рассмотрим задачу темы 3.8 о планируемом выпуске продукции.
F = 3х1 + 5х2 + 4х3 + 5х4 → max.

Построим двойственную ей задачу по следующим правилам.
Количество переменных в двойственной задаче равно количеству неравенств в исходной.
Матрица коэффициентов двойственной задачи является транспонированной к матрице коэффициентов исходной.
Столбец свободных членов исходной задачи является строкой коэффициентов для целевой функции двойственной. Целевая функция в одной задаче максимизируется, в другой минимизируется.
Условиям неотрицательности переменных исходной задачи соответствуют неравенства-ограничения двойственной, направленные в другую сторону. И наоборот, неравенствам-ограничениям в исходной соответствуют условия неотрицательности в двойственной.

Заметим, что строки матрицы задачи I являются столбцами матрицы задачи II. Поэтому коэффициенты при переменных yi в задаче II - это, соответственно, коэффициенты i-го неравенства в задаче I.
Неравенства, соединенные стрелочками, будем называть сопряженными.