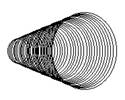
Будем называть поверхностью некоторую фигуру в пространстве, которую можно получить каким-либо перемещением обычной простой фигуры.

Построение поверхностей

 

Построение поверхностей можно также разделить на три этапа:

1 этап: выбор базовой фигуры

2 этап: определение начальных и конечных параметров базовой фигуры

3 этап: задание изменяемых величин и построение поверхности

Рассмотрим построение цилиндра, как наиболее простой фигуры.

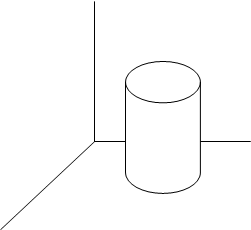
а) обозначим центр верхней части цилиндра

координаты точки: _______________

 

б) обозначим центр нижней части цилиндра

координаты точки: _______________

 

Мы видим, что у нас изменилась только координата Y

320,240

Следовательно, задав изменение этой координаты и записав

оператор построения эллипса в этих пределах мы получим ряд

эллипсов, которые визуально образуют цилиндр. Радиус

особого значения не имеет, важно лишь соблюсти соотно-

шение 1:2, характерное для «идеального» эллипса.

Построение поверхности:

y:=________;

while y<=________ do begin

ellipse(_____, y, 0, 360, 50, 25)

y:=y+3;

end;

 

Внешний вид цилиндра будет зависеть от значения шага изменения величины y.

 

Окончание программы стандартное:

 

readln;

closegraph;

end.

 

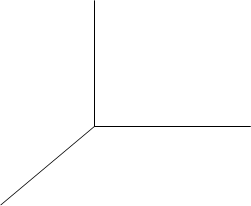Построим теперь более сложную поверхность, называемую однополостным гиперболоидом. Эта поверхность получается вращением параболы вокруг своей оси.

Посмотрите на рисунке эту фигуру и обозначьте ключевые параметры

для ее построения.

 

а) координаты центра верхней части __________________

 

б) координаты центра нижней части __________________

 

в) радиус верхней части __________

 

г) радиус нижней части __________

 

Мы видим, что помимо изменения координаты по оси Y у нас имеет место и изменение радиуса эллипсов, из которых получается наша фигура. Следовательно, нам необходимо найти зависимость величины радиуса от величины координаты.

 

Рассчитайте вместе с учителем зависимость радиуса от координаты и запишите основную

закономерность: _______________________________________________________________________

 

Запишем фрагмент программы для построения этой поверхности:

y:=________;

while y<=________ do begin

r:=______________________________;

ellipse(_____, y, 0, 360, r, round(r/2));

y:=y+3;

end;

 

Обратите внимание на то, что величины радиусов обязательно округляются.

 

По аналогичному принципу постройте следующие поверхности:

а) куб

б) однополостный параболоид (вращение правой или левой части параболы перпендикулярно ее оси)

Подсказки:

а) б)