Метод контурных токов

Методы контурных токов и узловых напряжений

Для разветвленных электрических схем метод уравнений Кирхгофа приводит к необходимости решения большого количества уравнений. Уменьшить количество уравнений анализа электрических цепей, отдельно метод контурных токов и узловых напряжений.

С помощью метода контурных токов анализируют цепи, решая не 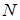уравнений (количество ветвей), а (количество независимых контуров) для схем, которые содержат идеальные и реальные источники напряжения (рисунок 2.5 и рисунок 3.7 соответственно). В схемах с источниками тока последние следует заменить эквивалентной схемой (рисунок 3.9).

Рассмотрим этот метод на примере схемы ( рисунок 3.11). Пронумеруем узлы и обозначим число независимых контуров:. Выберем для анализа независимые контуры . Зададим приблизительно направление тока в ветвях и направление обхода контуров.

 

 

Рисунок 3.11 Схема соединения сопротивлений и источников ЭДС

 

По второму закону Кирхгофа составим уравнение для первого контура:

Выразим токи «внутренних» ветвей через токи «внешних» цепей . По первому закону Кирхгофа для узлов и запишем:

; , откуда ; .

Тогда уравнение для первого контура примет вид:

.

 

Сгруппировав слагаемые с одинаковыми членами, получим:

. (3.10)

Введем понятия контурных токов, контурных ЭДС и сопротивлений. Контурный ток – ток в главной ветви, номер которой совпадает с номером контура и которая является внешней .

Другими словами, это токи внешних ветвей, которые как бы соединяются в соответствующих контурах. Для удобства будем считать, что направление контурного тока совпадает с направлением обхода соответствующего контура. В общем, контурные токи – это условные величины, но иногда они могут совпадать с токами ветвей схемы.

Контурная ЭДС -го контура равна алгебраической сумме всех ЭДС, которые входят в этот контур. Для рассмотренного примера:

; ; .

Собственное сопротивление -го контура равно сумме всех сопротивлений, которые образуют этот контур:

; ; .

Взаимное сопротивление -го и -го контуров равно сопротивлению ветви, которая входит в эти контура, со знаком “плюс”, если направления контурных токов в ней совпадают и со знаком “минус”, если они противоположны. Для схемы (рисунок 3.11) имеем:

; ; .

С учетом введенных обозначений, уравнение (3.10) будет таким:

Записав аналогично уравнения для второго и третьего контуров, получим систему уравнений, из которой можно определить любой контурный ток:

(3.11)

или в матричной форме:

(3.12)

где – квадратная симметричная матрица сопротивлений, число столбцов и строк которой равно ;

 

– матрицы – столбцы контурных токов и Э.Д.С. соответственно.

Также МКТ позволяет решить задачу анализа схемы с числом уравнений . Найдем из (3.2) первый контурный ток.

 

 

.

где – обозначение и алгебраическое дополнение матрицы резисторов.

Аналогично можно найти любой (– й) контурный ток в схеме:

, (3.13)

где – количество независимых контуров;;;

– обозначения и алгебраические дополнения матрицы резисторов;

– элемент матрицы - столбца контурных Э.Д.С.

Токи внутренних ветвей записываются как линейная комбинация контурных токов. Для схемы ( рисунок ) ; ; .