Контрольные задачи
Контрольные вопросы
2.3.1 В чем заключается отличие реальной от идеальной электрической цепи? Какие пассивные и активные элементы используются в теории цепей?
2.3.2 Что такое положительное направление тока? Какой вывод можно сделать, если после окончания расчетов ток имеет отрицательное значение?
2.3.3 Какими устройствами измеряют величину и направление постоянного тока и напряжения? Назовите параметры идеального амперметра и вольтметра?
2.3.4 Зависит ли выбор положительного направления напряжения от положительного направления тока?
2.3.5 Назовите идеальные пассивные элементы цепи. Какие физические аналоги соответствуют этим идеальным элементам?
2.3.6Поясните понятия линейной, параметрической и нелинейной индуктивности (емкости).
2.3.7 Чем отличаются зависимые и независимые источники энергии? Назвать виды управляемых источников тока и напряжения. Какой параметр является управляющим для каждого из этих источников?
2.3.8 Изобразить вольт - амперные характеристики идеального источника напряжения и тока. Сравните, чем отличаются ВАХ идеальных и реальных источников энергии?
Методические рекомендации.
Используя знания, полученные при изучении подразделов 2.1 и 2.2, решите нижеприведенные задачи и запишите их в тетрадь.
2.4.1 Начиная с момента 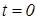 , через резистор
, через резистор 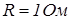 проходит ток
проходит ток 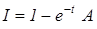 . Какое количество энергии выделится в виде тепла до момента времени, когда ток достигнет значения
. Какое количество энергии выделится в виде тепла до момента времени, когда ток достигнет значения  .
.
(Ответ: 0,168 Дж)
2.4.2 Начиная с момента 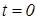 , через индуктивность
, через индуктивность  проходит ток
проходит ток 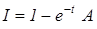 . Найти напряжение на индуктивности и энергию магнитного поля в момент времени, когда ток достигнет значения
. Найти напряжение на индуктивности и энергию магнитного поля в момент времени, когда ток достигнет значения  .
.
(Ответ: 0,37 В; 0,2 Дж)
2.4.3 Емкость  , которая имеет электрический заряд
, которая имеет электрический заряд  , в момент t = 0 начинает разряжаться через резистор
, в момент t = 0 начинает разряжаться через резистор 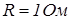 . Ток изменяется в соответствии с законом
. Ток изменяется в соответствии с законом  . Найти напряжение на емкости и энергию электрического поля в момент времени, когда ток достигнет значения
. Найти напряжение на емкости и энергию электрического поля в момент времени, когда ток достигнет значения  .
.
(Ответ: 37 В; 0,068 Дж)
Методические указания.
При изучении раздела 2.5 необходимо уяснить основные понятия элементов топологической структуры цепи. Необходимо разобраться, что же является контуром, узлом, ветвью. Далее необходимо разобраться в понятии «граф».
После этого следует сосредоточиться на изучении основных законов электрических цепей.
2.5 Схема электрической цепи. Основные топологические понятия ( ветвь, узел, контур электрической цепи). Понятие графа
Реальные электрические цепи представляются в виде моделей, в которых все элементы являются идеальными.
Электрическая схема представляет собой графическое изображение электрических цепей электронных, электро- или радиотехнических устройств, на котором условными обозначениями показаны элементы данного устройства и соединения между ними.
Топология схем – раздел, который изучает соединение между собой идеальных элементов электрической цепи.
Основные элементы топологической структуры цепи – ветвь, узел, контур. Рассмотрим на примере цепи:

Рисунок 2.7 Схема электрической цепи
Ветвь образуется одним или несколькими последовательно соединенными элементами цепи. При этом под последовательным соединением элементов цепи понимается такое соединение, при котором через все эти элементы проходит один и тот же ток.
Узел – место соединения трех или большего числа ветвей.
Ветви, присоединенные к одной паре узлов, называют параллельными.
Любой замкнутый путь, проходящий по нескольким ветвям, называется контуром.
В зависимости от числа контуров, имеющихся в схеме, различают одноконтурные и многоконтурные схемы. Одноконтурная схема является простейшей. Обозначим количество узлов через  , количество ветвей – через
, количество ветвей – через 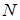 . Для вышеприведенной схемы
. Для вышеприведенной схемы  .
.
Топологические графы электрической цепи.
Граф – совокупность отрезков и линий произвольной длины и формы, соединенных определенным образом. Отрезки и линии называются ветвями графа, точки соединения ветвей – узлами графа. Граф, который может быть изображен на плоскости без пересечения дуг (ветвей), называется планарным графом
Топологический граф электрической цепи – условное графическое изображение электрической цепи, в котором показана лишь ее топология. Направление ветви графа определяется направлением тока соответствующей ветви электрической цепи.
Ветвь называется инциндентной узлу, если она подсоединена к нему. Два графа, имеющие одинаковое количество ветвей и узлов, одинаковым образом соединенных называются изоморфными. Деревом графа называется подграф (часть графа), в которую входят все узлы и не входит ни одного контура. Ветви графа, не входящие в состав дерева, называются главными ветвями дерева или хордами. Подключение к дереву каждой из главных ветвей создает по одному независимому контуру. Совокупность главных ветвей дерева называется дополнением дерева. Число главных ветвей дерева равно числу независимых контуров. Способ выбора независимых контуров: чертится дерево схемы и затем поочередно добавляются главные ветви. Любой контур, образуемый добавлением новой ветви, является независимым, так как он отличается от предыдущих контуров новой ветвью. В итоге, кода к дереву добавляются все главные ветви, получится граф схемы и число независимых контуров достаточным для расчета цепи. На рисунке показан планарный граф вышеприведенной схемы и два из возможных деревьев графа.

Рисунок 2.8 Топологическое изображение электрической цепи
 – количество ветвей дерева графа,
– количество ветвей дерева графа, 
 – количество главных ветвей дерева графа,
– количество главных ветвей дерева графа, 
Основные законы электрических цепей.
Анализ цепи – определение электрического положения цепи, т. е. определение токов и напряжений в ветвях цепи по известным значениям параметров цепи.
Синтез цепи – определение топологии цепи и значений параметров идеальных элементов цепи, которые позволяют получить заданную характеристику.
Рассмотрим три основные закона теории электрических цепей.
Основными законами теории электрических цепей наряду с законом Ома являются законы баланса токов в разветвлениях (первый закон Кирхгофа) и баланса напряжений на замкнутых участках цепи (второй закон Кирхгофа).
Первый закон Кирхгофа.
Алгебраическая сумма мгновенных значений токов в узле в любой момент времени равна нулю. При этом будем считать входящие в узел токи положительными, а выходящие из узла – отрицательными.


Суммирование распространяется на токи в ветвях, сходящихся в рассматриваемом узле. При этом знаки берутся с учетом выбранных положительных направлений токов.
Для схемы, изображенной на рисунке 2.7 составим уравнения по первому закону Кирхгофа.
Для каждого из узлов схемы получим следующие уравнения:




Количество независимых уравнений, которые составляются на основе первого закона Кирхгофа равно количеству ветвей дерева графа:


где  – количество уравнений, составляемых по первому закону Кирхгофа,
– количество уравнений, составляемых по первому закону Кирхгофа,  – количество узлов в электрической цепи.
– количество узлов в электрической цепи.
В данном случае  (сумма левых частей уравнений для четырех узлов равна нулю, т. е. одно уравнение лишнее).
(сумма левых частей уравнений для четырех узлов равна нулю, т. е. одно уравнение лишнее).
Первый закон Кирхгофа выражает тот факт, что в узле электрический заряд не накапливается и не расходуется. Сумма электрических зарядов, приходящих к узлу, равна сумме зарядов, уходящих от узла за один и тот же промежуток времени. Первый закон Кирхгофа применим не только к узлу, но и к любому контуру или замкнутой поверхности, охватывающей часть электрической цепи, так как ни в каком элементе цепи, ни в каком режиме электричество одного знака не может накапливаться.
Второй закон Кирхгофа
Алгебраическая сумма ЭДС в любом замкнутом контуре цепи равна алгебраической сумме падений напряжения на всех элементах этого контура в любой момент времени:


где  – количество ЭДС, действующих в контуре,
– количество ЭДС, действующих в контуре,  – количество пассивных элементов контура.
– количество пассивных элементов контура.
Обход контура совершается в произвольно выбранном направлении, например, по ходу часовой стрелки. Падения напряжений и ЭДС, направление которых совпадает с направлением обхода контура, берут со знаком “плюс”, а все напряжения и ЭДС противоположного направления берут со знаком “минус”. Значения напряжений записываются в одной части уравнения, а значения ЭДС – в другой. Для вышеприведенной схемы получим следующие уравнения:
I контур:  ;
;
II контур: 
III контур:  .
.
Алгебраическая сумма напряжений на ветвях в любом замкнутом контуре равна нулю.
Чтобы узнать, сколько уравнений необходимо составить для данной цепи по второму закону Кирхгофа, пользуются следующей формулой:


где  – количество независимых уравнений, составляемых по второму закону Кирхгофа,
– количество независимых уравнений, составляемых по второму закону Кирхгофа, 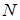 – количество ветвей,
– количество ветвей,  – количество узлов.
– количество узлов.