Метод Рунге-Кутта.
Метод Эйлера относится к семейству методов Рунге-Кутта.
Метод Рунге-Кутта  -го порядка имеет вид:
-го порядка имеет вид:
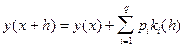 ,
,
где при фиксированных значениях некоторых параметров:
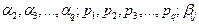

последовательно вычисляются:

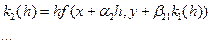

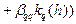
Наибольшее применение на практике получил метод Руте-Кутта 4-го порядка:
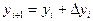 ,
,
где
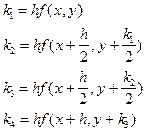
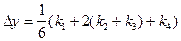
Метод Рунге-Кутта имеет ряд важнейших достоинств:
1) высокая точность
2) явная схема вычислений  за определенное количество шагов и по определенным формулам.
за определенное количество шагов и по определенным формулам.
3) возможен переменный шаг, т.е. можно сменить шаг, где функция быстро меняется.
4) легко оформляется.
Пусть дано дифференциальное уравнение:
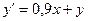

с начальными условиями:
 .
.
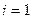
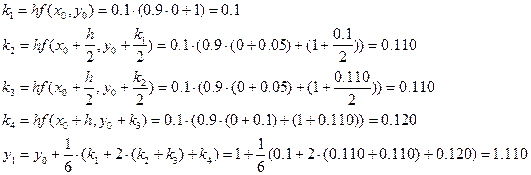
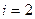
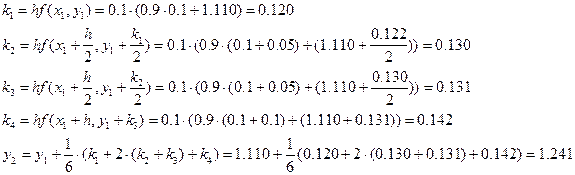
Решение ОДУ имеет вид:

| 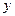
|
| 0.0 | 1.000 |
| 0.1 | 1.110 |
| 0.2 | 1.241 |