Условная вероятность. Теорема умножения вероятностей
Пусть на пространстве элементарных событий некоторого вероятностного эксперимента определены события А и В, причем P(B) ¹ 0.
Условной вероятностью события A при условии B (обозначается P(A|B)) называется …………………………………………………….................. ………………………………………………………………………………………
По определению ………………………………….. (1)
Вычисление условных вероятностей – это, по существу, переход в новое, урезанное заданным условием B пространство элементарных исходов. Вероятности элементарных событий P(wi) (wiÎB) пропорциональны исходным. Для соблюдения условия нормировки в новом пространстве элементарных исходов они делятся на P(B).
Аналогично определяется условная вероятность P(B | A):
.…………………………… если ………… (2)
Пример 7. Е: Подбрасывание двух монет. Рассматриваются события:  - выпадение герба на первой монете;
- выпадение герба на первой монете; 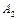 - выпадение герба на второй монете;
- выпадение герба на второй монете;  – выпадение двух гербов. ………………………………………………
– выпадение двух гербов. ………………………………………………
Вычислим условные вероятности:
………………… ………………… …………………
………………… ………………… …………………
………………… ………………… …………………
Формулы (1) и (2) часто записывают в виде
……………..………………………………….
и называют теоремой умножения вероятностейдля двух событий.
Теорема умножения вероятностей для трех событийимеет вид:
……………………………………………………..
Для произвольного числа n событий A1, A2,… An теорема умножения вероятностей имеет вид
……..………………………………………………………………………………...
То есть вероятность совместного появления нескольких событий равна ...................................................................................................................................... ...................................................................................................................................... ...................................................................................................................................... ...................................................................................................................................... ......................................................................................................................................
Пример 8. Студент пришел на экзамен, зная из тридцати вопросов программы только 25. В билете три вопроса. Найти вероятности следующих событий: В – студент сумеет ответить на все 3 вопроса, содержащиеся в билете; С - студент сумеет ответить на 2 вопроса их трех; D – студент сумеет ответить хотя бы на один из вопросов, содержащихся в билете.