Аксиомы теории вероятностей

Вероятность. Методы определения вероятностей

Проверочный тест 3

Свойства операций над событиями

………………………………………………………………………………............

Вероятностью события называется ……………………………………. ………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

Вероятность события А обозначается .........; от латинского probabilitas

Сформулируем основное положение теории вероятностей. Пусть дано дискретное пространство элементарных исходов W с элементами w₁, w₂, w₃,… Полагаем, что каждому из элементарных исходов w_i поставлена в соответствие некоторая неотрицательная числовая характеристика p_i = P(w_i), называемая вероятностью этого исхода, причем

.....................................................................

По определению,…………………………………………………………... ….….……………………………………………………….………………………………………………………………………………………………………………

………………………………

Рассмотрим аксиомы, которым должны удовлетворять вероятности любых событий:

А1 (Аксиома неотрицательности)……………………………………… ………………………………………………………………………………………

…………………………………

А2 (Аксиома нормированности)…………………………………………. ..………………………………………………………………………………….

……………………

А3 (Аксиома аддитивности)…………………………………………...….. …………………………………………………………………………………..…………………………………………………………………………………………….

……….....................................................................................

(С аксиоматическим построением ТВ для непрерывных пространств элементарных исходов можно познакомиться, например, в пособии: Гаврилюк А.А., Старовойтов А.Н. Методы теории вероятностей. – Гомель: БелГУТ, 2010 с . 29-31.)

Основные следствия из аксиом теории вероятностей:

1. Вероятность невозможного события……………………………….

…………………

2. Вероятность любого случайного события ……………………… ………………………………………………………………………………………

…………………….

3. Вероятность события 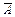, противоположного событию A, равна:

.………………….