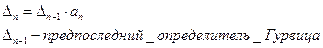Алгебраический критерий устойчивости Гурвица

Критерий устойчивости

Я проблема решается с применением Теоремы Ляпунова

Смысл теорем Ляпунова в том, что они дают критерий, когда устойчивость линейной влечет устойчивость исходной нелинейной.

Теорема 1(об устойчиовсти): Если линеаризованная система ассимптотически устойчива, то исходная нелинейная также устойчива., если возмущенные Н.У. сколь угодны малы.

Теорема 2( о неусточивости): Если линеаризованная система неутсойчива, то исходная нелинеейная также неустойчива

Теорема 3( критический случай): Если линеаризованная система нейтрально устойчива, то для суждения о устойчивости требуется отдельное исследование системы.

1. Алгебраический критерий устойчивости Гурвица. Частные случаи.

При высоком порядке характеристического уравнения трудно определить его корни.

Критерий устойчивости- приемы или методы исследования устойчивости без определения корней характеристического уравнения замкнутой АС. Критерии устойчивости бывают: алгебраическими и частотными

Известно Характеристическое уравнение замкнутой АС

Строим определитель Гурвица n-ого порядка. Строится следующим образом: 1-я строка коэффициенты с нечетными индексами. 2-я строка и последующие с индексами на 1 меньше. Если индес отрицательный или больше n то он равен 0.

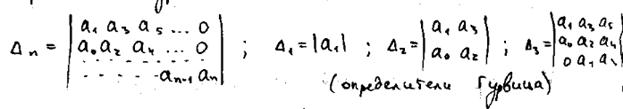
Необходимое и достаточное условие для устойчивости замкнутой АС по критерию Гурвица: необходимо и достатосно чтобы все определители Гурвица были положительными.

Частные случаи:

1. Необходимое условие устойчивости- для устойчивости замкнутой АС необходимо чтобы все коэффициенты замкнутой АС были положительными

2. Если