ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ МИКРОДВИГАТЕЛЕЙ ПОСТОЯННОГО ТОКА

ЛЕКЦИЯ №3

У исполнительных микродвигателей постоянного тока время протекания электромагнитных переходных процессов значительно меньше, чем время протекания электромеханических процессов. Поэтому динамические свойства исполнительного микродвигателя при переходных процессах можно исследовать с помощью уравнения равновесия моментов

,

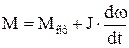где М– вращающий момент двигателя; М_ст– статический момент сопротивления на валу; J – момент инерции ротора. Для упрощения анализа принимаем М_ст = 0. Тогда

.(1.25)

Из выражения (1.25) видно, что изменение угловой скорости ротора ω во времени определяется законом изменения вращающего момента от угловой скорости, т.е. механической характеристикой.

Рассмотрим механическую характеристику исполнительного микро­двигателя постоянного тока при произвольном значении коэффициента сигнала α (рис. 1.8). На этой характеристике выберем точку С с текущими координатами: М(момент) и ω (скорость). Из подобия треугольников ABC и АВ'С' получаем

, (1.26)

где ω_0α и М_пα – значения скорости холостого хода и пускового момента при коэффициенте сигнала α.

Решаем уравнение (1.26) относительно М, подставляем в (1.25) и получаем дифференциальное уравнение движения ротора:

. (1.27)

При якорном управлении, согласно уравнению (1.27),

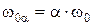; (1.28)

.(1.29)

Теперь уравнение (1.27) принимает вид

. (1.30)

 

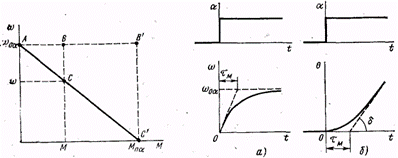
Рис. 1.8 Рис. 1.9

 

В случае полюсного управления значение М_пαможно определить также из выражения (1.29), а значение ω_0α – из (1.18):

. (1.31)

Подставляем (1.29) и(1.31) в (1.27) и получаем

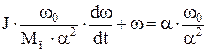. (1.32)

Решение уравнений (1.30) и (1.32) для режима пуска имеет вид

(.(1.33)

Выражение (1.33) есть уравнение переходной характеристики, т.е графика изменения во времени выходной величины ω при подаче, на вход некоторого постоянного сигнала α (рис. 1.9, а). Величина τ_м, входящая в выражение (1.33), – это электромеханическая постоянная времени двигателя, равная коэффициентам припроизводной от угловой скорости в уравнениях (1.30) и (1.32). Согласно(1.33), τ_м – это время, в течение которого электродвигатель после подачи напряжения управления развивает угловую скорость ротора, равную 0,632 от установившегося значения, соответ­ствующего норме.

Как видно из (1.27),

. (1.34)

При якорном управлении τ_м определяется выражением

, (1.35)

а при полюсном – выражением

, (1.35')

где ω₀/М_п=R_я/(kФ)².

На основании выражений (1.35) и (1.35') можно сделать вывод: электромеханическая постоянная времени прямо пропорциональна моменту инерции ротора, скорости холостого хода и обратно пропорциональна пусковому моменту. В случае якорного управления величина τ_м не зависит от коэффициента сигнала, а в случае полюсного – возрастает с уменьшением сигнала. Последнее объясняется уменьшением жесткости механических характеристик. От статического момента нагрузки на валу двигателя величина τ_м не зависит.

Из уравнений (1.30), (1.32) и (1.33) видно, что исполнительный микродвигатель постоянного тока является апериодическим звеном первого порядка, если за входную величину принять коэффициент сигнала α, а за выходную – угловую скорость ротора ω. Передаточная функция, соответствующая уравнениям (1.30) и (1.32),

. (1.36)

Коэффициент передачи двигателя k_дв соответственно при якорном и полюсном управлениях равен коэффициентам ω₀ и ω₀/α² при коэффициенте сигнала управления α в правых частях уравнений (1.30) и (1.32). Если скорость входит в уравнения в относительных единицах, то значения коэффициентов передачи определяются выражениями (1.12') и (1.20) при М^∂=0,так как сами уравнения (1.30) и (1.32) составлены для режима холостого хода.

Если в качестве выходной величины исполнительного микродвигателя рассматривать не угловую скорость, а угол поворота ротора θ(dθ/dt=ω),то двигатель является инерционным интегрирующим звеном, т. е. величина θ пропорциональна интегралу от входной величины (коэффициента сигнала α) по времени. Это видно из уравнения, которое получается на основании выражений (1.30) и (1.32) с учетом (1.33) и (1.34):

. (1.37)

Значения τ_м и k_двв (1.37) выбирают в соответствии со способом управления. Уравнение переходной характеристики, представленной на рис. 1.9, б, находят как решение дифференциального уравнения (1.37):

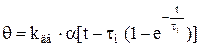. (1.38)

Передаточная функция, соответствующая уравнению (1.37),

. (1.39)

Из уравнений (1.30), (1.32) и (1.37) видно, что динамические свойства исполнительного микродвигателя постоянного тока существенно зависят от значения электромеханической постоянной времени. Чем меньше τ_м, тем микродвигатель ближе по своим свойствам к идеальному безинерционному звену. Уменьшение τ_м повышает быстродействие микродвигателя, т.е. сокращает промежуток времени между изменением сигнала на обмотке управления и достижением заданной скорости или угла поворота ротора.

Основные меры по уменьшению τ_м следующие:

1) снижение момента инерции ротора (если у микродвигателей с барабанным ротором τ_м составляет 0,035 – 0,15 с, то у микродвигателей с полым немагнитным ротором она снижается до 0,015 – 0,02 с, у микродвигателей с дисковым ротором – до 0,005 – 0,02 с);

2) увеличение пускового момента за счет совершенствования конструкции, применения лучших магнитных материалов и повышения плотности тока в обмотках.

Изложенный анализ динамики исполнительного микродвигателя постоянного тока проводился без учета электромагнитной постоянной времени, определяющей время протекания электромагнитных переходных процессов в обмотке управления. Однако в тех случа­ях, когда-электромагнитная постоянная времени соизмерима с элек­тромеханической (например, в малоинерционных исполнительных микродвигателях с полюсным управлением), при анализе динамики следует учитывать электромагнитную постоянную времени.