Риск и доход инвестиционного портфеля3
Инвестиционное решение для одиночного актива
В основе принятия решения о выборе того или иного варианта инвестирования лежит одна из основных гипотез (концепций) финансового менеджмента – гипотеза о несклонности инвесторов к риску (см. первую главу). Гипотеза утверждает позитивное соотношение между риском, ассоциируемым с инвестицией и ожидаемым доходом (доходностью): чем выше инвестиционный риск, тем выше ожидаемый инвестором доход.
На основе сформулированной гипотезы решение о выборе одной из двух инвестиционных альтернатив сводится к простым логическим рассуждениям2. В случаях, когда распределение доходов является нормальным (колоколообразным), ожидаемый доход и дисперсия полностью определяют характер распределения. Тогда справедливо следующее очевидное правило: инвестиция А предпочтительнее инвестиции В, если ожидаемый доход на А выше или равен ожидаемому доходу на В при том, что дисперсия А ниже дисперсии В; либо если ожидаемый доход на А превышает ожидаемый доход на В при том, что дисперсия А не выше дисперсии В.
Если распределение доходов не является нормальным, то приведенное выше правило может не сработать. В такой ситуации полезным может оказаться коэффициент вариации. Правило отбора здесь достаточно простое: актив с меньшим значением коэффициента вариации является более привлекательным с точки зрения инвестирования.
Простота приведенных выше логических рассуждений и сделанных выводов могут создать обманчивое впечатление тривиальности всего проведенного анализа. Следует, однако, иметь в виду, что основной целью анализа является не разработка конкретных рекомендаций инвестору (трудно предположить, что инвестор, выбирая объект инвестирования, осознанно руководствуется описанными процедурами), а прояснение финансовой природы принимаемых инвестиционных решений. В то же время из приведенных рассуждений следует весьма важный в плане управления рисками вывод о невозможности снижения рисков инвестиций в единичный актив без соответствующего снижения ожидаемой доходности.
Проведенный выше для одиночного актива анализ достаточно легко обобщить на случай инвестиционного портфеля. Ожидаемый доход Řp инвестиционного портфеля, состоящего из n активов, каждый соответственно c ожидаемым доходом Ři и удельным весом в портфеле wi, можно выразить формулой:
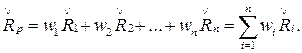 (3.7)
(3.7)
При этом необходимо иметь в виду, что удельные веса рассчитываются не от номинальной, а от рыночной стоимости соответствующих инвестиций, и сумма всех весов равна единице.
Определим несколько новых понятий. Под флуктуацией инвестиционного актива, в частности ценной бумаги, будем понимать изменение во времени полного дохода (доходности) на этот актив. Степень совпадения флуктуации двух активов в одном или противоположных направлениях, называется корреляцией. Статистической мерой корреляции является коэффициент корреляции, который будем обозначать ρ либо ρij, где номера i и j относятся к соответствующим активам. Коэффициент корреляции теоретически может лежать в пределах от –1 до + 1. В первом случае мы имеем строго негативную корреляцию, во втором – строго позитивную. Нулевой коэффициент корреляции означает, что доходы на рассматриваемые активы не коррелируют между собой. Соответствующие иллюстрации представлены на рис. 3.1, 3.2, 3.3.
На практике достижение как строго позитивной, так и строго негативной корреляции между инвестиционными активами вряд ли возможно. Примером позитивной корреляции могут служить доходы на акции компаний, работающих в одной отрасли и в одном регионе либо одной стране (последнее необходимо для того, что избежать влияния ряда рисков, включая политические). С известной долей осторожности можно утверждать, что негативно коррелируют между собой доходности обыкновенных акций и облигаций[29].

Рис. 3.1. Строго позитивная корреляция (ρ=1)

Рис. 3.2. Строго негативная корреляция (ρ=-1)
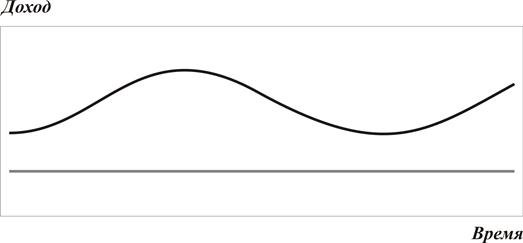
Рис. 3.3. Нулевая корреляция (ρ=0)
Введенный выше коэффициент корреляции тесно связан с другой величиной, используемой для описания того, насколько две величины "ковариируют" друг с другом – ковариацией σij. Обозначая через σi и σj соответственно стандартные отклонения доходности активов с номерами i и j, выражение для ковариации можно представить в виде:
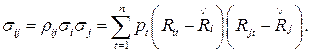 (3.8)
(3.8)
Отметим, что равенства (3.8) позволяют выразить коэффициент корреляции через ковариацию и стандартные отклонения. Таким образом, ковариация позволяет учесть не только относительное поведение доходностей двух активов, но и уровень риска, присущий каждому из активов. Последний выражается амплитудой колебаний доходности активов во времени, которая в свою очередь характеризуется стандартными отклонениями σi и σj.
Несложный анализ показывает, что ковариация может принимать как положительные, так и отрицательные значения. Если два актива имеют в целом позитивную корреляцию, то и отклоняться от ожидаемого значения они будут в одном направлении (положительном либо отрицательном), а значит их произведения, стоящие в правой части выражения (3.8), будут положительны. Наоборот, при негативной корреляции эти произведения будут отрицательны, что приведет к отрицательному значению всей суммы. Если изменение доходности обоих активов носит случайный характер, положительные и отрицательные слагаемые в правой части выражения (3.8) будут гасить друг друга, и значение ковариации окажется близким к нулю. Нулевым значение ковариации будет и в случае, когда хотя бы один из активов является безрисковым (см. рис. 3.3).