План-конспект занятия по русскому языку на тему: Язык как система.
ПРИЛОЖЕНИЕ Б
ПРИЛОЖЕНИЕ А
СПИСОК ЛИТЕРАТУРЫ
Вопросы для самопроверки
1. В чём заключаются градиентные методы поиска экстремума? Как осуществляется движение к экстремуму с помощью метода градиента?.
2. Чем отличается метод наискорейшего спуска от метода градиента?
3. Какие особенности обобщённого метода Ньютона и метода Гаусса – Зайделя?
4. В каких случаях используются методы определения градиента? Опишите метод численного дифференцирования.
5. В чём заключается метод синхронного детектирования? Каким образом получается выражение для градиента? Постройте структурную схему.
6. Какой принцип построения поисковых СНС с оптимизацией качества управления с настройкой по внешним воздействиям? Какие зависимости критериев оптимизации используются при проектировании поисковых СНС?
7. Какой принцип работы схемы поисковой СНС с оптимизацией качества управления с настройкой по характеристикам объекта управления?
1. Романенко В.Д., Игнатенко Б.В.Адаптивное управление технологическими процессами на базе микроЭВМ. - К.: Вища школа, 1990. - 334 с.
2. Чураков Е.П.Оптимальные и адаптивные системы: уч. пос. - М.: Энергоатомиздат, 1987. - 256 с.
3. Александров А.Г.Оптимальные и адаптивные системы: Учебн. пос. – М.: Электронная книга, 2003. - 278 с.
4. Александров А.Г.Оптимальные и адаптивные системы: Учебн. пос. для вузов по спец. "Автоматика и упр. в техн. сист.". – М.: Вища школа, 1989. - 263 с.
5. Попович М.Г., Ковальчук О.В.Теорія автоматичного керування: Підручник / За ред. Мнишенко А.С. - К.: Либідь, 1997. - 544 с.
(справочное)
А.1. РАЗЛОЖЕНИЕ ФУНКЦИИ В РЯД ТЕЙЛОРА
Функцию 
в окрестностях точки 
можно разложить в ряд Тейлора по формуле:
.
Тогда разложение в ряд Тейлора для разности функций
.
Если в (6.24) принять 
; 
; 
, то
.
А.2. СВОЙТВА ФУНКЦИИ СИГНУМ
Используемая в п.п.7.2-7.4 функция сигнум имеет следующие свойства:
; 
.
А.3. ДОКАЗАТЕЛЬСТВО ВЫРАЖЕНИЯ (12.25)
При 
.
При 
.
(справочное)
РЕШЕНИЕ УРАВНЕНИЙ ГАМИЛЬТОНА-ЯКОБИ (7.16), (7.17)
Пусть объект управления описывается уравнениями состояния (7.13):
; 
; 
, (Б.1)
где управление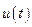 
может принимать два значения: 
.
Вначале примем 
.
Поделив почленно одно уравнение на другое, исключаем переменную 
:
. (Б.2)
Проинтегрируем (Б.2):
, (Б.3)
где 
- постоянная интегрирования.
 |
Таким образом, решениям уравнений состояния (Б.1) соответствует семейство парабол в фазовой плоскости
, каждая из которых является фазовой траекторией этой системы (рис. Б.1).
Рисунок Б.1 – Фазовая траектория системы (Б.1) при
Проведя аналогичные рассуждения при 
, получим
. (Б.4)
Предположим, что оптимальное движение фазовой точки начинается из точки 
в начало координат 
и происходит вначале по параболе из семейства (Б.4) при (рис. Б.2).
Поскольку точка находится на параболе, то для точки можно записать, что
,
а парабола, проходящая через точку , определяется уравнением
. (Б.5)
 |
Рисунок Б.2 – Оптимальное движение фазовой точки
Для того чтобы фазовая точка попала в точку , предположим, что после пересечения с параболой из семейства (Б.3) при дальнейшее оптимальное движение происходит по параболе
, (Б.6)
которая проходит через начало координат.
Обозначим точку пересечения парабол 
.
Определим ординату 
точки 
, подставив (Б.6) в (Б.5).
; 
.
Время движения фазовой точки из 
в при можно определить из уравнения
,
после интегрирования которого получим 
; 
.
Время движения фазовой точки из в начало координат 
при можно определить из уравнения
.
Откуда следует, что 
; 
.
Тогда полное время движения фазовой точки
. (Б.7)
Если движение начинается вначале по параболе из семейства (Б.3) при , а потом продолжается по параболе (Б.4) при , то выполнив аналогичные операции, получим выражение
. (Б.8)
Как видно из выражений (Б.7) и (Б.8) время движения фазовой точки в начало координат зависит только от координат начальной точки. Так как в качестве начальной точки может быть выбрана любая точка фазовой плоскости, определяемая уравнениями состояния (Б.1), то получим выражения (7.18).
Язык – душа нации. Язык – это есть живая плоть идеи, чувства, мысли.