Аналитические СНС с настройкой по внешним воздействиям

ТЕМА 11 АНАЛИТИЧЕСКИЕ СНС С ОПТИМИЗАЦИЕЙ КАЧЕСТВА УПРАВЛЕНИЯ

Вопросы для самопроверки

1. Как классифицируются СНС с моделью? Каким образом можно синтезировать СНС со стабилизацией качества управления с эталонной моделью, используя метод Ляпунова?

2. Какие особенности СНС с настраиваемой моделью?

3. Какие принципы и схемы используются при синтезе СНС со стабилизацией АЧХ?

4. Какая методика синтеза СНС со стабилизацией импульсной характеристики?

 

 

В отличие от СНС со стабилизацией качества управления СНС с оптимизацией качества должны постоянно определять и поддерживать оптимальные значения критерия качества при измеряющихся свойствах ОУ и внешних воздействиях. Если бы изменения свойств ОУ и внешних воздействий не происходило, то достаточно было бы один раз рассчитать оптимальные параметры и структуру УУ, используя принцип оптимального управления. При построении СНС этот этап называется этапом первичной оптимизации системы. При изменении свойств ОУ и внешних воздействий параметры УУ уже не будут оптимальными в новых условиях и необходимо снова перестраивать параметры УУ, т.е. необходимо осуществлять самонастройку системы. Этап самонастройки системы называют этапом вторичной оптимизации системы. Поскольку этап первичной оптимизации в достаточно полном объёме рассмотрен при проектировании оптимального управления, то остановимся на втором этапе.

Аналитические СНС с настройкой по внешним воздействиям должны выполнять две основные функции:

1) определять и анализировать изменения внешних воздействий;

2) разрабатывать алгоритмы оптимизации системы по критерию самонастройки (вторичной оптимизации) при изменении внешних воздействий. Поэтому в аналитические СНС с настройкой по внешним воздействиям входит анализатор сигналов (АС) и управляющий элемент (УЭ).

Как отмечалось ранее (см. п.9.2) в зависимости от того, какой параметр анализируется (полезный сигнал и воздействия или результат их воздействия) схемы аналитических СНС делятся на схемы СНС с идентификационным (разомкнутым циклом самонастройки) и безыдентификационным (замкнутым циклом самонастройки) подходами (рис. 11.1).

 

 

 

а) б)

Рисунок 11.1 – Схемы аналитических СНС:

а) с идентификационным подходом;

б) с безыдентификационным подходом,

где АС – анализатор сигналов;

ВО – вычислитель ошибок;

УЭ – управляющий элемент.

 

При идентификационным подходе с помощью АС оцениваются параметры и вероятностные характеристики полезного сигнала 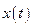и возмущений и . Управляющий элемент по результатам анализа АС рассчитывает и устанавливает оптимальные параметры УУ. При этом сигнал не подаётся на устройство адаптации (АС+УЭ) (рис. 11.1, а). Такая схема называется схемой с разомкнутым циклом самонастройки.

Если выходной сигнал подаётся на УА (рис. 11.1, б), то такая схема называется схемой с замкнутым циклом самонастройки. В этом случае в вычислителе ошибок (ВО) анализируются последствия воздействия полезного сигнала и возмущений, то есть и , и вырабатывается сигнал, пропорциональный отклонению параметров УУ от оптимальных значений. УЭ, воздействуя на УУ, сводит эти отклонения к минимуму.

Эти оба подхода являются частичными случаями схем разомкнутого и замкнутого циклов самонастройки соответственно.

В качестве примера рассмотрим методику определения оптимальных параметров УУ аналитической СНС с оптимизацией качества управления с настройкой по внешним воздействиям при разомкнутой схеме самонастройки (при идентификационном подходе) (см. рис. 11.1, а).

В этом случае общепринято критерий качества самонастройки определять по формуле:

, (11.1)

где - динамическая ошибка, обусловленная неточностью воспроизведения системой полезного сигнала 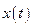(например, переходные процессы);

- случайная составляющая ошибки, вызванная внешними возмущениями и ;

- дисперсия случайной составляющей ошибки в момент времени ;

- коэффициент, регулирующий вес обеих ошибок.

Обозначим варьируемые параметры УУ, являющиеся аргументами критерия качества самонастройки , через вектор .

Динамическая ошибка определяется по формуле

, (11.2)

где - порядок полинома, используемого при аппроксимации входного сигнала .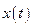

Коэффициенты ошибок , , …, определяются по формуле:

. (11.3)

Следовательно, , .

Теперь определим . Для этого запишем передаточные функции основного контура, представленного на рис. 11.2

 

Рисунок 11.2 - Структура основного контура системы

 

Из рис. 11.2 видно, что уравнение, описывающее объект управления, можно представить в операторной форме:

, (11.4)

где , , - некоторые операторы.

Тогда передаточные функции

; ; .

Введём переменную . С учётом этого передаточные функции ошибки относительно внешних воздействий примут вид:

;

;

.

Дисперсия случайной составляющей ошибки определяется по формуле:

, (11.5)

где и - спектральные плотности процессов и соответственно;

.

Интеграл (11.5) удобно вычислить, используя формулу (8.15):

.

Подставив выражения (11.2) и (11.5) в выражение для критерия качества самонастройки (11.1), устанавливается в явной форме зависимость критерия от вектора параметров . После оценивания блоком АС характеристик воздействий определяются оптимальные значения варьируемых параметров из условия равенства нулю частичной производной от по :

.