БИЛЕТ 5) 2.2 Уравнения системы в нормальной форме Коши

В теории автоматического управления (ТАУ) систему из сложных нелинейных дифференциальных уравнений высоких порядков принято преобразовывать в систему дифференциальных уравнений первого порядка. Из (1.1) видно, что система описывается 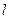– дифференциальными уравнениями 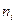порядка. Их можно представить в виде системы из дифференциальных уравнений первого порядка, каждое из которых разрешено относительно производной. Для этого вводят новых переменных , , …, , которые подбираются так, чтобы систему (2.1) можно было представить в виде:

(2.2)

Такая система дифференциальных уравнений первого порядка (2.2) называется системой уравнений в нормальной форме Коши.

Тогда выходные параметры ОУ

. (2.3)

Уравнения (2.2) и (2.3) называются уравнениями состояния.