Алгоритм для нестационарного режима.

Алгоритм неявного метода.

1. задание вектора неизвестных т-р начального приближения, К – шаг итерации.

 

 

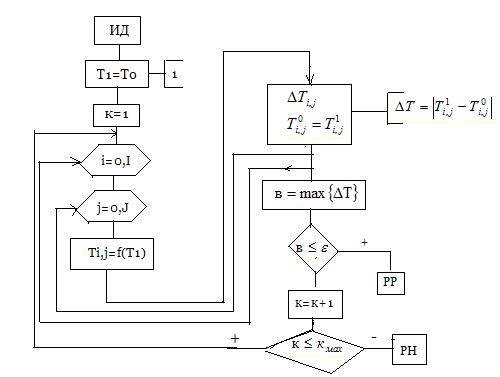
if (i=0 and j=0) then T[i,j].

if (i>1 and i<21 and j>1 and j<21) Then T[i,j].

2.

 

 

При рассмотрении метода конечных разностей. Мы не обращали внимания на влияние пар-ров сетки на численное решение. Часто предполагают, что более высокую точность решения можно получить простым уменьшением шага сетки, соответственно, увеличивая объем работы. В дей­ствительности не всегда так, и кроме того, нам нужно получить правильный рез-т при мини­мальных затратах, поэтому важно знать не только сам метод, но и уметь определять его св-ва. Основными св-ми численных методов считают устойчивость, точность и сходимость.

Схема численного метода считается неустойчивой, если сеточное решение стационарного у-ния теплопроводности или другого вида переноса имеет колебательный хар-р или для неста­ционарного у-ния приобретает колебательный хар-р, и при этом ошибка постоянно возрастает и становится неограниченной. Для исследования устойчивости разработаны спец. методы: в ча­стности метод дискретных возмущений. Этот метод закл-ся в том, что в конечно-разностные у-ния вводятся некоторые возмущения, и далее определяются, при каких условиях это возмуще­ние могут затухать.

В качестве примера рассм-м нестационарное линейное у-ние теплопроводности:

, которое может быть представлено в виде: .

 

Если .

У-ние будет устойчиво в том случае, когда: .

Если: , тогда у-ние будет устойчиво при .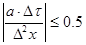

Точность метода определяется точностью аппроксимации исходного у-ния конечно-разност­ного у-ния:

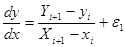
, , . Погрешность м.б. разной.

Ф-ция точки: .

- ошибка будет пропорциональна 1-й степени нашего интер­вала.

Разложим в обратную сторону:

.

Сложим 1 и 2:

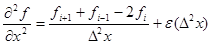- вторая производная.

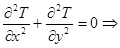
+=0, .

Метод аппроксимации:

.

Запись для этих 3 точек значения ф-ции:

Конечно-разностная схема считается сходимой, когда выполняется условие сходимости в виде:

, где - решение системы к-ой итерации, - решение системы на к+1-ой итерации.

Конечно-разностные схемы так же хар-ся понятием консервативности, которое закл-ся в том, что при получении конечно-разностных у-ний выполняется условие соблюдения исходных ин­тегральных законов сохранения, справедливых для исходных диф. у-ний.

В противном случае говорят о дивергентной форме конечно-разностных у-ний.