ОГРАНИЧЕННЫЕ СВЕДЕНИЯ О СТАТИСТИЧЕСКИХ ХАРАКТЕРИСТИКАХ

 

Рассмотрим теперь случай, когда в соответствии с § 3.1 ограниченные априорные сведения о l заключаются в знании ряда статистических характеристик l (а не полного распределения вероятности), таких, как среднего значения, дисперсии, корреляционной матрицы и т. д., то есть математических ожиданий некоторой совокупности функций l. Класс r_о возможных распределений вероятности l в этом случае определен с помощью ограничений (3.1.4), где

(5.4.1)

индекс k пробегает столько значений, сколько задано условий. В остальном же плотность распределения р(l) остается произвольной.

Для отыскания минимаксного правила решения с учетом заданных .ограничений на класс r_о возможных распределений вероятности l вос­пользуемся соотношением (5.1.1) и найдем наименее предпочтительное распределение из этого класса. Тогда байесово правило решения для этого распределения l будет минимаксным. Ограничимся случаем не­прерывных множеств l и u.

Пусть u = u₀(х,p) - байесово правило решения относительно неко­торого априорного распределения l, с плотностью р(l)Îr_о, получаемое с помощью обычной процедуры минимизации среднего риска R(u(х),р).Используем для отыскания наименее предпочтительного распределения метод Лагранжа, позволяющий учесть ограничения (3.1.4) на класс допустимых распределений вероятности. При этом плотность наименее предпочтительного распределения р*(l)определяется из условия максимума функционала:

(5.4.2)

где u = u₀(x,р), а c₀, c_k - неопределенные множители, выбор которых должен обеспечить выполнение заданных ограничений (3.1.4) на p(l), то есть

(5.4.3)

(a_k - заданные значения математических ожиданий функций f_k(l)).

Вычислим вариацию функционала I(p) по функции р(l)

(5.4.4)

где d_р(l) - вариация функции p(l);d_рu₀ - вариация решающей функ­ции u₀(x,р) по функции p(l), которая, очевидно, не зависит явно от l, а зависит только от х; Ñ_ug(u,l) - градиент функции потерь по реше­нию u. Поскольку в (5.4.2), (5.4.4) u = u₀(х, р), то есть является байесовой решающей функцией относительно распределения l с плотностью р(l) и минимизирует средний риск

то из условия обеспечения минимума R(u(х),p) для этого решения следует выполнение равенства

. (5.4.5)

Поэтому второе слагаемое в (5.4.4) обращается в нуль при любой р(l). Из условия обращения в нуль вариации среднего риска (5.4.4) следует уравнение для условного риска

(5.4.6)

которое позволяет сформулировать следующее правило нахождения наименее предпочтительного распределения:

- для того чтобы распределение с плотностью вероятности р(l) = р*(l) было наименее предпочтительным в классе распределений r_о, удовлетворяющих заданным ограничениям (5.4.3), условный риск для байесова правила решения относительно этого распределения должен иметь функциональную зависимость от l, определяемую выражением (5.4.6).

Это утверждение обобщает требование независимости условного риска от l, вытекающее из теоремы Вальда, при полном отсутствии априорных сведений о l. Последнее является естественным частным случаем (5.4.6), когда ни одной функции f_k(l) - не задано и сумма по l в правой части (5.4.6) отсутствует. Конкретный вид наименее предпо­чтительного распределения (плотности р*(l)) и соответствующего ему минимаксного правила решения зависит от заданных ограничений, а также от вида функции правдоподобия Р(х|l) и функции потерь g(u, l), однако соотношение (5.4.6) позволяет найти р*(l) и минимакс­ное правило решения для многих важных с практической точки зрения случаев.

Рассмотрим один из таких примеров, когда l={l₁, ... ... l_n} являет­ся n-мерным вектором, решение u = {u₁, ... ... u_n} - его оценкой, и задана корреляционная матрица l

,

а в остальном распределение l неизвестно и может быть произвольным.

При этом f(l) = {l_nl_m } - совокупность всех произведений l_n и l_m (n,m=1,…,n), а уравнение (5.4.6) для условного риска принимает вид

(5.4.7)

где множители c₀ и c_nm (n,m = 1,…,n) определяются из условий

(5.4.8)

Таким образом, оценка u = u(x), соответствующая ограниченным априорным знаниям только корреляционной матрицы l, является опти­мальной, если она байесова относительно априорного распределения вероятности l, для которого корреляционная матрица равна заданной, а условный риск для этой оценки представляет собой сумму постоянной, величины и квадратичной формы l, вида

.

Покажем, что при некоторых предположениях наименее предпочти­тельным является нормальное распределение l. Пусть функция потерь квадратичная, то есть

(5.4.9)

где g = ||g_nm|| - произвольная матрица, и пусть существует достаточная статистика z = z(x), для которой хотя бы приближенно

(5.4.10)

где А=||A_nm||, detA - определитель матрицы А. (При этом без ограни­чения общности можно полагать М{l} = 0.) Достаточная статистика z(x) является оценкой максимального правдоподобия вектора l, а пред­ставление (5.4.10) требует, чтобы она была несмещенной (M{z} = l) и распределена нормально (хотя бы приближенно). Матрица А в (5.4.10) - это так называемая информационная матрица Фишера, которая определяется следующим образом:

(5.4.11)

где математическое ожидание вычисляется при фиксированном l. Она. характеризует рассеяние оценки максимального правдоподобия и потен­циально достижимую точность оценивания l в отсутствие всяких апри­орных сведений о l. Обратная ей матрица А^-1 является корреляционной матрицей ошибок для эффективной оценки l, которой при данном пред­ставлении Р(z|l) является оценка максимального правдоподобия - до­статочная статистика z(x).

Рассмотрим нормальное распределение вероятности l с корреля­ционной матрицей R и найдем для него байесову оценку. Средний риск в этом случае равен

(5.4.12)

где R^-1 - матрица, обратная R, и в силу того, что z = z(x) является достаточной статистикой и оптимальное решение u = u(x) может зави­сеть от х только посредством z = z(x), осуществлен переход от полной совокупности данных наблюдения х к достаточной статистике z - оцен­ке максимального правдоподобия вектора l. Минимум среднего риска (5.4.12) достигается, если u является условным (при заданном значе­нии z) математическим ожиданием l, то есть байесово правило решения имеет вид

(5.4.13)

где матрица C =||C_nm||, определяется уравнением

. (5.4.14)

Найдем теперь условный риск для этого правила решения:

, (5.4.15)

где I - единичная матрица; , а - след матрицы ().

Как видно из (5.4.15), условный риск имеет требуемый вид (5.4.7). Это означает, что нормальное распределение вероятности является наименее предпочтительным, а сама оптимальная оценка имеет вид (5.4.13), то есть является линейным преобразованием оценки максималь­ного правдоподобия. Матрица линейного преобразования С зависит от корреляционной матрицы R вектора l и корреляционной матрицы А^-1 ошибок для оценки вектора l методом максимального правдоподобия. Минимаксный риск для заданного класса r₀ распределений вероят­ности l имеет следующее значение:

(5.4.16)

где SpCA^-1g - след матрицы CA^-1g, то есть сумма ее диагональных элементов. Он всегда меньше минимаксного риска при полном отсутст­вии сведений об априорном распределении l, который в условиях спра­ведливости (5.4.10) равен SpCA^-1g. Значение риска (5.4.16) для правила решения (5.4.13) достигается, очевидно, также при любом распределе­нии р(l), для которого корреляционная матрица равна R.

Представление функции правдоподобия (5.4.10) заведомо выполняется в том случае, когда х = {x₁,..., х_n} и x_v=l_n+x_n, a {x_n} - совокупность нормальных случайных величин с корреляционной матрицей R_x = А^-1, то есть если данные наблюдения х представляют собой аддитивную смесь век­тора l с гауссовой помехой x = {x₁,..., x_n}.

Если при этом известна корреляционная матрица l, то этому слу­чаю соответствует известная постановка задачи линейной фильтрации. Ее винеровское решение имеет вид (5.4.13), (5.4.14), а полученные выше результаты позволяют установить минимаксный смысл этого решения: если никаких других сведений о l, кроме корреляционной матрицы, нет, то никакого лучшего (в смысле квадратичной функции потерь) по срав­нению с линейным оператором (5.4.13) оператора фильтрации не су­ществует и только более подробные статистические сведения могут привести к изменению структуры оптимального оператора фильтрации.

Можно проиллюстрировать использование уравнения (5.4.6) для нахождения минимаксных оптимальных оценок еще большим количест­вом случаев. Например, пусть индекс n для l_n и u_n, имеет смысл дискретного времени и для всех n = 2,…,n заданы средние квадраты изменения за один шаг, то есть

(5.4.17)

При переходе к непрерывному времени это будет означать задание среднего квадрата производной процесса l (t) для любого момента вре­мени в интересующем нас интервале.

Уравнение (5.4.6) при этих ограничениях на распределение l при­нимает вид

Если задан второй момент для начального значения s²₁ = M{l²₁}, то к правой части этого выражения следует прибавить еще один член c₁l²₁. Аналогично рассмотренному выше случаю можно убедиться, что при этих ограничениях наименее предпочтительным является распре­деление для марковской случайной последовательности l = {l₁, ... l_n} с переходной плотностью вероятности

(5.4.18)

и с равномерным распределением для начального значения l₁, когда величина s²₁ = M{l²₁} не задана, либо нормальным распределением вероятности для l₁ с дисперсией s²₁, если последняя задана. В обоих случаях оптимальная минимаксная оценка (оптимальный алгоритм фильтрации) находится без труда с помощью достаточно разработан­ных для подобных задач методов получения байесовых оценок.

 

5.5. ЗАМЕЧАНИЯ О ХАРАКТЕРЕ НАИМЕНЕЕ ПРЕДПОЧТИТЕЛЬНОГО РАСПРЕДЕЛЕНИЯ

 

Во всех предыдущих примерах наименее предпочтительное распре­деление вероятностей l обладает характерной особенностью - оно является распределением с максимальной для заданного класса r₀ энтропией, то есть его плотность р*(l) удовлетворяет соотношению

. (5.5.1)

Этим свойствам обладает равномерное для всех значений l распределе­ние при полном незнании статистики l, равномерное на множестве значении L: l = f(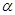) - распределение при ограничении допустимых значений l совокупностью гиперповерхностей l = f(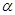), нормальное рас­пределение при задании только корреляционной матрицы и т. д.

Можно высказать гипотезу, что и в других случаях наименее пред­почтительным распределением является распределение с максимальной энтропией. Хотя доказать такую гипотезу или установить достаточно общие условия, при которых она справедлива, довольно затруднитель­но, однако она обладает большой степенью правдоподобия. Поэтому, да­же несколько вольное ее использование для более широкого круга задач, в которых прямо найти наименее предпочтительное распределение не удается, представляется довольно конструктивным. Это конструктивное содержание заключается в несравнимо большей простоте решения уравнения (5.5.1) для нахождения распределения с наибольшей энтро­пией.

Воспользуемся этой гипотезой для нахождения решения одной задачи распознавания образов при полном отсутствии априорной ин­формации, в том числе и в отношении статистического описания данных наблюдения х. Пусть наблюдается некоторая совокупность признаков двух объектов, так что x = {x₁, x₂}, где x₁ - наблюдаемая совокупность признаков первого объекта, х₂ - второго. Сами объекты могут быть либо одинаковыми (обозначим это состояние l = 1), либо как-то раз­личаться (l = 2), и на основании данных наблюдения {х₁, х₂} нужно решить, какое именно состояние имеет место, то есть принять одно из двух возможных решений: u₁ - объекты одинаковы, u₂ - объекты различны. При этом будем считать, что априорные вероятности состояний

p(l = 1) = Р₁ ,

p(l = 2) = Р₂ = 1-P₁ ,

а также распределения вероятности при­знаков х (функция правдоподобия) совершенно неизвестны. Несмотря на такую крайнюю степень априорной неопределенности, задача все-та­ки имеет решение, поскольку она содержит некоторую, правда, весьма нечеткую априорную информацию, скрытую в самой ее постановке, предположение о том, что статистические свойства совокупностей x₁ и x₂ могут быть либо различными, либо одинаковыми.

Предположим, что все наблюдаемые признаки объектов имеют только дискретные значения. Тогда можно занумеровать эти значения общей нумерацией от единицы до некоторого значения N и без огра­ничения общности заменить все множество признаков одномерной ве­личиной с возможными целочисленными значениями от 1 до N. Полное статистическое описание этого множества заключалось бы в задании распределения вероятностей этих значений, то есть вероятностей p_i (i = l, ..., N), причем если объекты различны (l = 2), то эти веро­ятности для совокупностей данных x₁ и х₂ будут иметь разные значения:

(5.5.2)

Если объекты одинаковы, то одинаковы и эти значения

(5.5.3)

Пусть далее совокупности данных наблюдения x₁ и х₂ первого и второго объектов представляют собой n₁- и n₂-кратные повторения наблюдений признаков этих объектов. Обозначим через n_1i и n_2i число раз, когда для первого и второго объектов соответственно наблюда­лось i-e значение признаков. При этом

(5.5.4)

Совокупности данных наблюдения x₁ и х₂, очевидно, могут быть описаны совокупностью значений чисел { n_1i } и { n_2i }, то есть

 

. (5.5.5)

Если вероятности p_1i, p_2i известны, то эти совокупности описываются мультимиальными распределениями вероятности следующего вида:

(5.5.6)

На самом деле вероятности p_i, p_1i, p_2i (i = l, ..., N), а также априорные вероятности состояний P₁ и P₂ неизвестны, и для получения решения задачи нужно найти наименее предпочтительные вероятност­ные меры, определенные на множестве этих неизвестных величин. Сово­купность этих вероятностных мер включает: m₀(P₁, P₂) - для априор­ных вероятностей состояний, которая определена на множестве значений Р₁ и P₂, удовлетворяющем условию Р₁ + P₂=1, m₀(p₁, p₂,…, p_N) - для вероятностей значений признаков, если объекты одинаковы (эта мера определена на множестве значений p₁, p₂,…, p_N, ограниченном условиями (5.5.3)); m( p₁₁, p₁₂,…, p_1N, p₂₁, p₂₂,…, p_2N) - для вероятностей значений признаков, если объекты различны (эта мера определена на множестве значений p₁₁, p₁₂,…, p_1N, ограниченном условиями (5.5.2)).

Используем для нахождения всех этих мер высказанную выше гипотезу. Из принципа максимума энтропии вытекает равномерность m₀, которая после усреднения величины среднего риска с произвольными: значениями Р₁ и Р₂ приводит к подстановке значений

(5.5.7)

в выражении для среднего риска. Мера m₁ также равномерна на мно­жестве, заданном условиями (5.5.3), что приводит к следующему зна­чению функции правдоподобия для i = l:

(5.5.8)

Мера m₂ получается в виде произведения двух мер, одна из которых равномерна на множестве , а другая - на множестве , что приводит к следующему выражению для значения функции правдоподобия при l = 2:

(5.5.9)

которое, естественно, не зависит от индивидуальных значений n_1i, n_2i. Отношение правдоподобия, которое с учетом (5.5.7) для простой функции потерь g(u, l) = g( u = j, l = I) = l - d_ij при сравнении с поро­гом, равным единице, дает окончательный вид правила принятия реше­ния об одинаковости объектов, будет иметь значение

(5.5.10)

При изменении функции потерь или задании априорных вероятностей-состояний P₁ и Р₂, отличных от (5.5.7), изменяется только величина порога С в правиле L₁₂(x) > C принятия решения u₁. Вид достаточной статистики L₁₂ (x) =L₁₂ (n₁₁, n₁₂,…, n_1N, n₂₁, n₂₂,…, n_2N) из (5.5.10) при этом остается неизменным. Таким образом, правило решения u(х) в рассмат­риваемых условиях полной априорной неопределенности будет иметь следующую структуру:

(5.5.11)

где L₁₂(x) определяется выражением (5.5.10). (Для исключения неко­торой нечеткости вида этого правила, связанной с возможностью получить значение L₁₂(x) = C, можно любое из неравенств в (5.5.11) дополнить равенством или принять при L₁₂(x) = C решение наугад.)

При больших значениях n_1i, n_2i выражение для отношения прав­доподобия (5.5.10) можно заметно упростить, а если еще предположить, что возможные различия между объектами не очень велики (это наи­более трудный для правильного решения случай), то L₁₂ (x) можно представить в виде монотонной функции следующей достаточной ста­тистики:

(5.5.12)

сравнение которой с порогом и дает требуемое правило решения. Вели­чина z(x) совпадает с величиной c² для достаточно известного критерия c-квадрат, основанного на среднеквадратичном различии двух вы­борочных распределений.В данном случае этот критерий полу­чается как асимптотическое приближение (при n_1i >> 1, n_2i >> 1) решения (5.5.10), (5.5.11), пригодного для любых значений n_1i, n_2i.

Полученное решение легко обобщается на более сложные задачи распознавания образов со многими альтернативами в условиях полной априорной неопределенности. Пусть, например, имеется не два, а т объектов, которые все могут быть одинаковыми, разными или образовы­вать некоторое число l групп, каждая из которых содержит объектов (l = 1 - все объекты одинаковы; 1 = m, все m_j = 1 и все объекты различны). Для каждой из таких гипотез подобно (5.5.6) можно без труда записать значение функции правдопо­добия этой гипотезы при известных распределениях вероятности наблю­даемых признаков, а затем аналогично (5.5.8), (5.5.9) произвести их усреднение по соответствующим мерам, равномерным на ограниченных множествах значений этих вероятностей. В итоге получаются выражения, подобные (5.5.8), (5.5.9) и содержащие произведения факториалов для сгруппированных соответствующим образом чисел наблюдений каждого значения признака (i = l, ..., N). Совокупность этих вы­ражений и будет являться достаточной статистикой.