Начальные понятия

Граф состоит из двух множеств – множества V, элементы которого называются вершинами, и множества Е, состоящего из пар вершин, эти пары называются ребрами графа. Это записывают так: G = (V, E), где G – имя графа.

Один момент в этом определении требует уточнения: считаем ли мы ребра 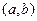и 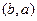различными. Если да (и это распространяется на все ребра), то граф называется ориентированным (сокращенно орграф), в противном случае ­– неориентированным.

Говорят, что ребро соединяет вершины а и b. Если такое ребро в графе есть, то говорят, что вершины а и b в нем смежны. Заметим, что в графе может быть не более одного ребра, соединяющего данную пару вершин. Ребро типа 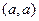, т.е. соединяющее вершину с ней же самой, называют петлей.

Говорят, что ребро 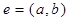инцидентно каждой из вершин а и b, а каждая из этих вершин инцидентна ребру е.

В дальнейшем, если не оговаривается иное, под графом понимается неориентированный граф без петель, такие графы называют обыкновенными. Для обозначения числа вершин и числа ребер графа будем обычно использовать буквы 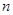и .

Мультиграф – обобщение понятия графа. В мультиграфе могут быть кратные ребра, то есть несколько ребер, соединяющих одну и ту же пару вершин. Иначе говоря, в мультиграфе Е является мультимножеством, то есть одна пара может входить в него несколько раз.

Способы задания графов

Существует много способов представить граф, назовем только самые распространенные.

1. Перечисление элементов. Исходя из определения, для того, чтобы задать граф, достаточно перечислить его вершины и ребра (т.е. пары вершин).

2. Изображение. Если граф невелик, его можно нарисовать. В неориентированном графе ребра изображаются линиями, в ориентированном – стрелками.

3. Матрица смежности. Пусть G – граф с n вершинами, пронумерованными числами от 1 до n. Матрица смежности – это таблица с n строками и n столбцами, в которой элемент, стоящий на пересечении строки с номером i и столбца с номером j, равен 1, если вершины с номерами i и j смежны, и 0, если они не смежны.

4. Матрица инцидентности. Пусть G – граф, вершины которого пронумерованы числами от 1 до n, а ребра – числами от 1 до m. В матрице инцидентности строки соответствуют вершинам, а столбцы – ребрам. На пересечении строки с номером i и столбца с номером j стоит 1, если вершина с номерами i инцидентна ребру с номером j смежны, и 0 в противном случае.

5. Списки смежности. Этот способ часто используется для компьютерного представления графов. Состоит он в том, что для каждой вершины задается список всех смежных с ней вершин. В структурах данных, применяемых в программировании, списки смежности могут быть реализованы как массив линейных списков. При решении задач будем эти списки оформлять так: пишется номер или имя вершины и после двоеточия перечисляются все смежные с ней вершины.